kinematika-jednačine kretanja
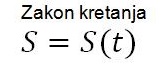
Kinematika je dio teorijske mehanike koji proučava kretanje
tijela ne uzimajući u obzir njihovu masu i sile koje dejstvuju
na njih. Kretanje tijela se vrši tokom vremena u prostoru, pa
kinematika ima dvije osnovne veličine: put s
i vrijeme t. Njihove osnovne jedinice su metar i
sekunda. U klasičnoj mehanici vrijeme je pozitivna skalarna
veličina koja se stalno mijenja, pa se uzima za nezavisno promjenljivu.
Sve ostale veličine u kinematici se posmatraju kao funkcije vremena.
Razlikuju se početno vrijeme (početak kretanja) t0
, proteklo (od starta) vrijeme ti i interval
vremena Δt=i+1 - ti-1.
Za definiciju kretanja u kinematici se, osim osnovnih, koriste i
izvedene veličine: ubrzanje a i brzina v.
Ubrzanje je promjena brzine u intervalu vremena a=Δv/Δt.
Brzina je pređeni put u intervalu vrremena v=Δs/Δt.
U kinematici se posmatra kretanje krutih tijela, tj. tijela koja ne
mijenjaju svoj oblik (ne deformišu se). Kretanje nekog tijela je poznato
ako je tokom vremena poznat položaj svake tačke tog tijela. Zbog
toga se kinematika bavi kretanjem i tačke i tijela, pa se ona i
dijeli na: kinematiku tačke i
kinematiku krutog tijela
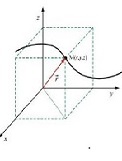
Položaj tačke u nekom trenutku zadaje se u Dekartovom
sistemu, sa koordinatnim početkom
O
i tri međusobno upravne ose
xyz. Putanja
(trajektorija) tijela je neprekidna linija koju opisuje težište
tijela pri kretanju u odnosu na Dekartov koordinatni sistem.
Težište je zamišljena tačka u kojoj djeluje
težina tijela.
Prema položaju trajektorije razlikuju se
- kretanje u ravni
- kretanje u prostoru
Prema obliku putanje kretanje se dijeli na:
- pravolinijsko kretanje
- krivolinijsko kretanje
Prema brzini kretanje može biti:
-
ravnomjerno ili jednoliko (brzina ne mijenja ni intenzitet
ni pravac)
-
ubrzano ili promjenljivo (brzina mijenja intenzitet i/ili
pravac)
Pravolinijsko kretanje može biti
jednoliko (brzina ne mijenja intenzitet)
i
promjenljivo (brzina mijenja intenzitet, postoji
ubrzanje).
Krivolinijsko kretanje je uvijek
promjenljivo, jer brzina mijenja
svoj pravac u prostoru tokom kretanja tijela.
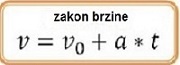
Pravolinijsko kretanje koje ima konstantno ubrzanje
a
naziva se
jednako ubrzano pravolinijsko kretanje.
Za njega zakon promjene brzine glasi:
v = v0 +
a*t.
Ako je poćetna brzina
v0=0 jednaka nuli,
onda zakon izgleda
v = a*t.

Jednačina zavisnosti puta od brzine za jednako ubrzano pravolinijsko
kretanje je
s = v0*t + a*t2/2.,
a ako je početna brzina jednaka nuli
v0=0
zakon pređenog puta glasi
s = a*t2/2.
 Vertikalni hitac naviše
Vertikalni hitac naviše je poseban slučaj jednako ubrzanog
pravolinijskog kretanja tijela u polju sile zemljine teže, sa početnom
brzinom
v0 ≥ 0. Ubrzanje vertikalnog
hica jednako je ubrzanju zemljine teže
g = 9,81 m/s i

suprotnog je smjera od brzine, što znači da je smanjuje. Kod
vertikalnog hica naviše ubrzanje uslijed sile gravitacije djeluje
kao
usporenje.
Kosi hitac je ravansko krivolinijsko kretanje tijela u polju
gravitacije sa početnom brzinom v0 ≥ 0.
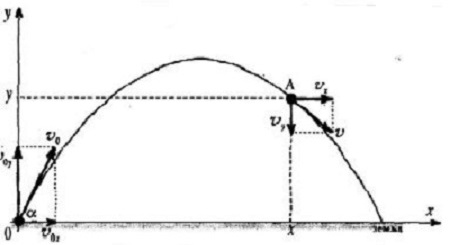 Tijelo se kreće pod uglom koji se posmatra u ondosu na horizontalni pravac.
Putanja tijela u slučaju kosog hitca je parabola. Odstojanje od koordinatnog
početka do padne tačke je domet XD.
Domet zavisi od početne brzine tijela v0 i od
ugla θ pod kojim hitac startuje(ugao elevacije).
Najviša tačka putanje naziva se tjeme putanje.
Tijelo se kreće pod uglom koji se posmatra u ondosu na horizontalni pravac.
Putanja tijela u slučaju kosog hitca je parabola. Odstojanje od koordinatnog
početka do padne tačke je domet XD.
Domet zavisi od početne brzine tijela v0 i od
ugla θ pod kojim hitac startuje(ugao elevacije).
Najviša tačka putanje naziva se tjeme putanje.
dinamika-sile, masa, inercija
Nije teško razlikovati objekat (tijelo) u kretanju i objekat koji miruje.
Nadzvučni avioni, sportski automobili ili biciklo mogu biti objekti u
kretanju ili mirovanju. Što uzrokuje da se jedan objekt kreće ili da
miruje? Što je razlog da se objekat u kretanju zaustavi?
 Odgovor je jednostavan. Uzrok je sila (force). Sila je bilo kakvo
dejstvo koje može učiniti da neko tijelo promijeni svoj oblik ili
kretanje.
Odgovor je jednostavan. Uzrok je sila (force). Sila je bilo kakvo
dejstvo koje može učiniti da neko tijelo promijeni svoj oblik ili
kretanje.
Dinamika je dio fizike (posebno klasične mehanike) koji se bavi
izučavanjem uticaja sila na kretanje materijalnih tijela. Temelje
dinamike postavio je Sir Isaak Newton definicijom
zakona kretanja. Dinamika, za razliku od kinematike uzima u obzir
tri fizička svojstva materijalnih tijela u dodiru, masu rakete m,
gustinu vazduha ρ kao i masu gasova koja ističe iz raketnog
motora ω.
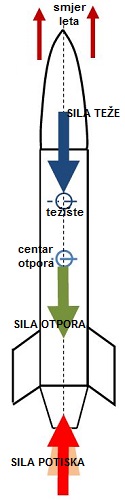 Tijelo rakete, vazduh i produkti sagorijevanja barutnog goriva djeluju
uzajamno. Produkti sagorijevanja potiskuju raketu dajući joj brzinu,
težina usporava raketu, a vazduh svojom gustinom stvara aerodinamičku
silu otpora koja takođe usporavaju raketu.
Tijelo rakete, vazduh i produkti sagorijevanja barutnog goriva djeluju
uzajamno. Produkti sagorijevanja potiskuju raketu dajući joj brzinu,
težina usporava raketu, a vazduh svojom gustinom stvara aerodinamičku
silu otpora koja takođe usporavaju raketu.
Sile koje djeluju na raketu u letu su:
- Sila potiska - T (thrust)
- Sila teže - W (weight)
- Sila otpora - D (drag)
Dejstvo sila na raketu je kompleksan fenomen. Da bi se pojednostavio
proračun putanje, stvara se uprošćen dinamički model kretanja
rakete. Model predpostavlja da:
-
Sila potiska djeluje saosno na raketu u smjeru kretanja,
u centru izlaznog presjeka mlaznika.
-
Sila otpora djeluje saosno na raketu u centru otpora rakete,
suprotnog smjera od smjera kretanja.
-
Sila teže djeluje u težištu rakete, saosno sa raketom,
suprotnog smjera od smjera kretanja.
-
Raketa se kreće vertikalno naviše u polju sile gravitacije
(putanja je vertikalni hitac) , sa početnom brzinom
v0 ≥ 0 .
-
Raketa se lansira sa nivoa mora. Temperatura vazduha je 20°.
Kretanja vazduha (vjetra) nema. .
-
Raketa je dealno uravnotežena. Težište se poklapa sa
koordinatnim početkom rakete. Uzdužna osa spoljnje konture je
identična sa uzdužnom koordinatnom osom rakete. Napadna tačka
sile potiska je tqkođe na uzdužnoj osi rakete. .
Model kretanja rakete ne dovodi do grešaka u proračunu, samo
ga čini jednostavnijim. Dobijeni rezultati parametara putanje
omogućavaju potpunu i realnu ocjenu ostvarenja ciljeva projekta.
Model idealizuje uslove u kojima se odvija kretanje rakete.
Uticaj stvarnih uslova razmatra se u završnoj fazi projekta.
Tada se unose korekcije i dopune u finalnu verziju konstrukcije.
Vertikalni hitac je pogodan za primjenu iz dva razloga.
Taj oblik putanje omogućava lakšu analizu (izračunavanja), a
osim toga takvu putanju imaju modelarske i istraživačke rakete.
Masa rakete je funkcija vremena,
m=f(t), u aktivnoj
fazi leta (dok radi raketni motor-sagorijeva gorivo i ističu produkti
gorenja). Na ostalom dijelu putanje (pasivni dio) ona je nepromjenljiva
m=const.
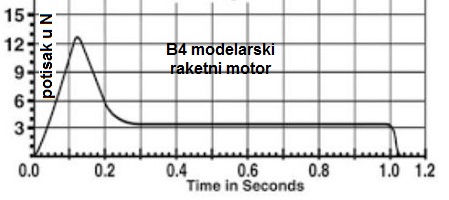
Promjena sile potiska u vrementu
T=f(t) je poznata
ili se odredi preliminarnim proračunima na osnovu zahtjeva
projekta. Promjena se daje u obliku dijagrama zavisnosti sile
potiska od vremena rada motora. Za modelarski motor totalnog
impulsa
Itot = 5Ns dijagram je dat na
prijethodnoj slici.
Postavljanjem fizičko modela kretanja rakete stvoraju se uslovi
da se proračunaju parametri (veličine) u svakoj tački putanje,
odnosno da se postave dinamičke jednačine kretanja.
Proračunom se određuju maksimalna brzina, promjena brzine tokom leta,
promjena visine tokom leta i maksimalna visina leta
Hmax.
.
primjena jednačina dinamike i proračun putanje
u više približenja od projektnih zahtjeva do konstrukcije rakete
 Svaka raketa se pravi sa ciljem da da se ostvare postavljeni projektni
zahtjeve. To mogu biti vrsta i količina korisnog tereta, visina
koja se treba dostići itd. U slučaju modelarske rakete projektni
zahtjevi su pravilan let i usporeno spuštanje na tlo. Modelarska
raketa zbog toga ima ima dobro projektovan stabilizator i padobran
kao korisni teret za bezbjedno spuštanje modela na tlo.
Realizaicja projekta rakete odvija se u nekoliko koraka.
Svaka raketa se pravi sa ciljem da da se ostvare postavljeni projektni
zahtjeve. To mogu biti vrsta i količina korisnog tereta, visina
koja se treba dostići itd. U slučaju modelarske rakete projektni
zahtjevi su pravilan let i usporeno spuštanje na tlo. Modelarska
raketa zbog toga ima ima dobro projektovan stabilizator i padobran
kao korisni teret za bezbjedno spuštanje modela na tlo.
Realizaicja projekta rakete odvija se u nekoliko koraka.
-
Definisanje korisnog tereta je početni korak. Procjenjuju se
vrsta, količina, oblik i dimenzije, količina (težina i
zapremina) itd.
-
Na osnovu poznatog korisnog tereta procjenjuju se
kostrukcija rakete (prečnici, dužine, debljine, raketni
motor, stabilizator itd).
-
Podaci dobijeni u koraku 2 omogućavaju da se ocijeni
preliminarna vrijednost pasivne težine rakete i dobije
poćetni oblik njenih konstrukcionih komponenti. Tako se
dobija mogućnost procjene aerodinamički i balističkih
karakteristika rakete, a sa time i mogućnost proračuna
putanje (maksimalne visine).
-
Korak 4 je traženje granica u kojima treba da se kreće
maksimalna brzina rakete. Zadaju se neke vrijednosti i
uz procjenu dužine aktivnog dijela puta izračunava
odgovarajuća maksmalna visina Hmax,.
Na osnovu dobijenih rezultata procjenjuje se vrijednost
maksimalne brzine rakete, kojom se ostvaruje projektom
zadata visina.
-
Slijedeći potez je da se na osnovu jednačine Ciolkovskog
izračuna količina raketnog goriva potrebna da se ostvari
brzina iz koraka 4. Time su dobijeni podaci potrebni
za prvi potpuni preliminani dinamički proračun putanje.
Na osnovu vrijednosti
Hmax, dobijene
proračunom, ocjenjuje aw koliko preliminarni podaci zadovoljavaju
projektne zahtjeve. Ako je
Hmax
manja od projektom postavljene,
razmatra se povećanje količine raketnog goriva. Razmatraju se i drugi
konstrukcioni parametri. Zatim se sa novim podacima ponovo ulazi u
proraćun maksimalne visine i tako više puta.
Ovaj postupak se naziva
približavanje projektom
zadatim vrijednostima. Kad se za parametre putanje (visinu), dobije
zadovoljavajući rezultat iterativni dinamički proračun je završen.
Zatim se pristupa detaljnoj definiciji konstrukcije rakete i sve
provjerava konačnim proračunom i prikladnim eksperimentima.
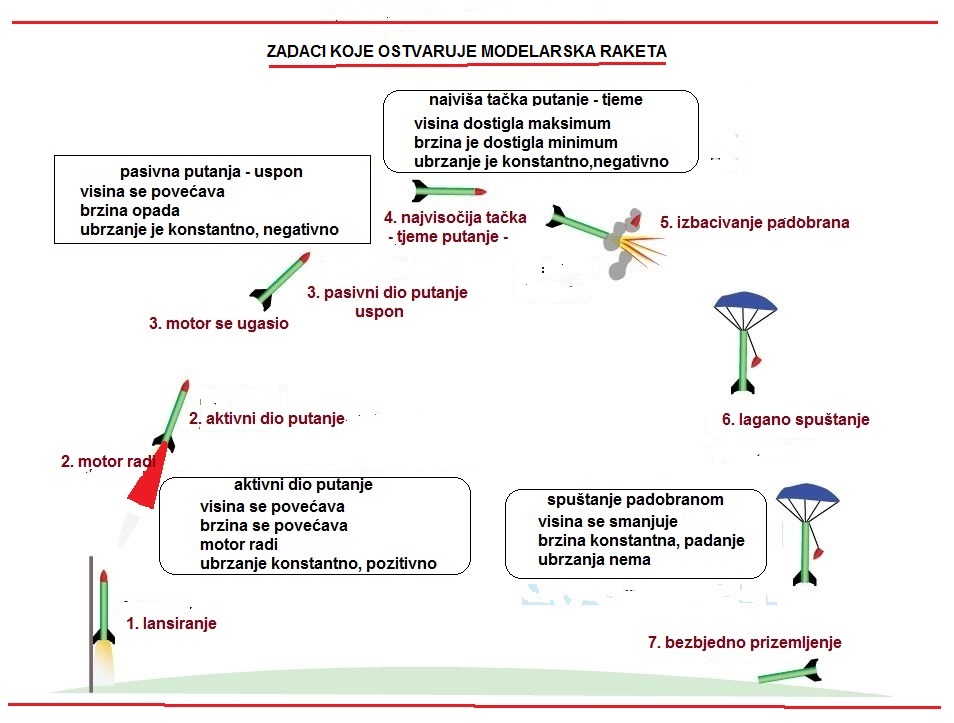
faze kretanja rakete na putanji
 U kretanju rakete razlikuju se tri faze:
kretanje kroz lanserni uređaj,
aktivni dio puta, i pasivni dio puta.
Pod aktivnim dijelom puta podrazumijeva se dio putanje na kojoj radi raketni
motor (dio puta na kojem sagorijeva raketno gorivo). Jedan dio aktivne
putanje obuhvata i kretanje rakete kroz lansirni uređaj. To je neslobodno,
vođeno kretanje.
Drugi dio aktivne putanje odvija se van lansera. To je slobodno
aktivno kretanje. Na aktivnom dijelu putanje raketa dobija ubrzanje pod
dejstvom sile potiska T raketnog motora.
Raketa mora napuštiti lanser sa brzinom koja je dovoljna za stabilan let
na nevođenom dijelu aktivnog puta. Brzina napuštanja lansera se naziva
početna brzina i označava sa v0.. Vrijednost
početne brzine zavisi od ubrzanja rakete a. Na osnovu
početne brzine određuje se dužina lansera. Preporuka je da raketa ima
ubrzanje a ≥ 15 m/s2 da bi bila stabilna
po izlasku iz lansera.
U kretanju rakete razlikuju se tri faze:
kretanje kroz lanserni uređaj,
aktivni dio puta, i pasivni dio puta.
Pod aktivnim dijelom puta podrazumijeva se dio putanje na kojoj radi raketni
motor (dio puta na kojem sagorijeva raketno gorivo). Jedan dio aktivne
putanje obuhvata i kretanje rakete kroz lansirni uređaj. To je neslobodno,
vođeno kretanje.
Drugi dio aktivne putanje odvija se van lansera. To je slobodno
aktivno kretanje. Na aktivnom dijelu putanje raketa dobija ubrzanje pod
dejstvom sile potiska T raketnog motora.
Raketa mora napuštiti lanser sa brzinom koja je dovoljna za stabilan let
na nevođenom dijelu aktivnog puta. Brzina napuštanja lansera se naziva
početna brzina i označava sa v0.. Vrijednost
početne brzine zavisi od ubrzanja rakete a. Na osnovu
početne brzine određuje se dužina lansera. Preporuka je da raketa ima
ubrzanje a ≥ 15 m/s2 da bi bila stabilna
po izlasku iz lansera.
Na kraju aktivnog puta raketa ima najveću brzinu Vmax
od tog momenta leti po inerciji. To je pasivni dio putanje, zato što nema
uticaja nikakve pogonske sile. Postoje samo aerodinamičke sile i sila
gravitacije. One usporavaju raketu (negativno ubrzanje).
uslovi i predpostavke
sile koje utiču na kretanje
U svakoj fazi leta na raketu djeluju sila potiska T,
sila aerodinamičkog otpora D i
sila gravitacije Q. Sila potiska T
daje raketi ubrzanje, sile D i Q
usporavaju raketu. Predpostavka je da su sve sile saosne osi
simetrije rakete i da nema nikakvih bočnih dejstava, koji bi
remetili let. Radi jednostavnije analize predpostavlja se da je
putanja rakete vertikalni hitac naviše. Kretanje je promjenljivo
pravolinijsko, jer se tokom leta stalno mijenja brzina (ubrzanje i
usporenje). Formula a = T/mR
daje ubrzanje rakete. Sila potiska u toj formuli određuje se iz
dijagrama sile potiska u funkciji vremena za primijenjeni raketni motor.
 Za modelarsku raketu to može biti dijagram promjene sile potiska
u funkciji vremena modelarskog raketnog motora B4.
Iz dijagrama sile potiska T = f(t) za
svako zadato vrijeme može se očitati vrijednost sile
T. Masa rakete mR se
mijenja na aktivnom dijelu putanje, zbog sagorijevanja raketnog
goriva. I sila potiska i masa rakete značajno se mijenjaju tokom
vremena. Da bi uticaj tih promjena na vrijednosti proračuna brzine
rakete i pređenog puta bio zanemarljiv, proračuni se vrše za jako
male intervale vremena. Ovakav pristup omogučava da se kretanje
rakete u postavljenom intervalu vremena posmatra kao jednako
ubrzano. Na osnovu jednačina koje važe za pravolinijsko jednako -
ubrzano kretanje mogu se izračunati brzina i put rakete u svakom
intervalu. Njihovim sabiranjem mogu se dobiti parcijalne, ali i
ukupna vrijednost. Ovakav pristup proračunu naziva se numerička
integracija diferencijalnih jednačina.
Za modelarsku raketu to može biti dijagram promjene sile potiska
u funkciji vremena modelarskog raketnog motora B4.
Iz dijagrama sile potiska T = f(t) za
svako zadato vrijeme može se očitati vrijednost sile
T. Masa rakete mR se
mijenja na aktivnom dijelu putanje, zbog sagorijevanja raketnog
goriva. I sila potiska i masa rakete značajno se mijenjaju tokom
vremena. Da bi uticaj tih promjena na vrijednosti proračuna brzine
rakete i pređenog puta bio zanemarljiv, proračuni se vrše za jako
male intervale vremena. Ovakav pristup omogučava da se kretanje
rakete u postavljenom intervalu vremena posmatra kao jednako
ubrzano. Na osnovu jednačina koje važe za pravolinijsko jednako -
ubrzano kretanje mogu se izračunati brzina i put rakete u svakom
intervalu. Njihovim sabiranjem mogu se dobiti parcijalne, ali i
ukupna vrijednost. Ovakav pristup proračunu naziva se numerička
integracija diferencijalnih jednačina.
aktivni dio putanje - kretanje u lanseru
Kretanje rakete počinje u lanseru iz stanja mirovanja . To znači
da je startna brzina vs = 0.
I startno vrijeme je ts = 0.
Lanser je postavljen vertikalno jer se razmatra vertikalni hitac.
Zanemaruju se sile trenja i druga dejstva koja mogu nastati
tokom kretanju kroz lanser i biti remetilački faktor.
Parametri vs i ts
su početne vrijednosti u proračunu kretanja kroz lanser.
Numerička integracija jedančina leta rakete u lanseru obavlja se
za male vremenske intervale, Δt = 0,001sec.
Integracijom se dobija put L, na kojem brzina ima vrijednost dovoljnu
za stabilan let. To je brzina napuštanja lansera,odnosno početna brzina
v0 slobodnog leta rakete.
Put koji odgovara brzini napuštanja lansera, je dužina vodilica
lansitnog uređaja L0. Istovremeno se
dobija i vrijeme prolaska kroz lanser. To vrijeme se
naziva početno vrijeme t0.
slobodna aktivna putanja - kretanje van lansera
Kao što su vs i startno vrijeme
ts polazna tačka za proračun
kretanja kroz lanser tako su i v0
, t0 i L0
polazina tačka za proračun elemenata slobodne aktivne putanje.
Na tom dijelu putanje rakete djeluju iste sile kao u slačaju kretanja
kroz lanser: sila potiska T,
sila aerodinamičkog otpora D i
sila gravitacije Q. Jedino nema vodilica koje
usmjeravaju kretanje rakete. Pretpostavka ja tokom aktivnog leta
nema bočnih udara koji bi djelovali kao remetilački faktor
(udari vjetra itd).Numerička integracija jedančina leta rakete na
ovom dijelu putanje takođe se obavlja za male vremenske intervale,
a preporuka je Δt = 0,01sec.
Na kraju aktivnog dijela putanje sila potiska raketnog motora
je T = 0. Raketa stiče maksimalnu brzinu
vmax. Numeričkom integracijom izračunavaju
se dužina (za vertikalni hitac naviše visina) aktivnog dijela
puta rakete Ha. i vrijeme potrebno da
se on pređe ta..
Maksimalna brzina rakete vmax, dužina
aktivnog dijela puta Ha i njegovo trajanje
ta određuju početnu tačku pasivnog dijela
putanje rakete. Numeričkom integacijom dobijaju se parametri ostalih
tačaka. Proračun se završava maksimalnom visinom leta, a to je
tjeme putanje HT.
U tjemenu je brzina kretanja v = 0,
pa se numerička integracija obavlja samo do te tačke. Pored
tjemena putanje tada se dobija i ukupno vrijeme leta rakete do
tjemena, tT.
Na pasivnom dijelu putanje raketa se kreće na osnovu Prvog Njutnovog
zakona, po inerciji. Nema sile potiska raketnogo
motora, T = 0. Kretanje se odvija samo pod
dejstvom aerodinamičkih sila i sile gravitacije.
To bi bio KRAJ proračuna parametara leta rakete u
izloženom primjeru
>
proračun putanje
jednačine
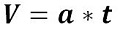
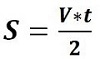 Kretanje rakete se posmatra kao pravolinijsko, jednako
ubrzano. Za njega kinematske jednačine brzine i pređenog
puta glase: v = a*t i S = v*t/2,
(v-brzina, S-put, a-ubrzanje i t-vrijeme).
Na rješavanje jednačina kretanja rakete primjenjuje se numerička
integracija. Numerička integracija razmatra veoma male intervale
promjena brzine i puta sa vremenom. Dovoljno male da aproksimacija
o pravolinijskom jednako ubrzanom kretanju daje zadovoljavajuće
rezultate. Jednačine kretanja primijenjene na male vremenske
intervale su date na slikama 3 i 4.
Kretanje rakete se posmatra kao pravolinijsko, jednako
ubrzano. Za njega kinematske jednačine brzine i pređenog
puta glase: v = a*t i S = v*t/2,
(v-brzina, S-put, a-ubrzanje i t-vrijeme).
Na rješavanje jednačina kretanja rakete primjenjuje se numerička
integracija. Numerička integracija razmatra veoma male intervale
promjena brzine i puta sa vremenom. Dovoljno male da aproksimacija
o pravolinijskom jednako ubrzanom kretanju daje zadovoljavajuće
rezultate. Jednačine kretanja primijenjene na male vremenske
intervale su date na slikama 3 i 4.
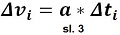
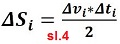 ΔSi je promjena puta u proizvoljnom
intervalu Δti , promjena brzine je
Δvi, a Δti
je proizvoljni interval vremena tokom numeričkog integraljenja putanje.
ΔSi je promjena puta u proizvoljnom
intervalu Δti , promjena brzine je
Δvi, a Δti
je proizvoljni interval vremena tokom numeričkog integraljenja putanje.
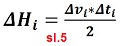 Ako se jednačine primijene na vertikalno, pravolinijsko, promjenljivo kretanje
onda je jednačina promjene puta (visine) ΔHi
kao na slici 5. Kinematske jednačine promjene visine i brzine rakete tokom
vertikalnog leta daju odnose brzine, ubrzanja, puta i vremena. Ako se zna
ubrzanje u nekom intervalu vremena može se izračunati prmjena brzine u
u tom intervalu,
Δvi = a*Δti .
Ako se zna promjena brzine može se izračunati pređena visina u tom intervalu
ΔHi = Δvi*
Δti/2.
Sabiranjem vremenskih intervala Δti
od početka kretanja do nekog proizvoljnog trenutka u toku leta
dobija se vrijeme leta ti do tog
trenutka. Sabiranjem promjena brzina
Δvi
u svim intervalima do nekog proizvoljnog intrvala i,
dobija se ukupna brzina u trenutku leta ti.
Sabiranjem promjena visine
ΔHi
u svim intervalima do nekog proizvoljnog intrvala i,
dobija se ukupna visina u trenutku leta ti.
Međutim, da bi se određivali pređeni put, brzina i vreijeme leta
potrebno je poznavati ubrzanje a kojem je podvrgnuta
raketa.
Prema Drugom Njutnovom zakonu ubrzanje, promjena brzine i
pravca su posledica dejstva spoljašnjih sila na tijelo, u ovom
slučaju raketu.
Ako se jednačine primijene na vertikalno, pravolinijsko, promjenljivo kretanje
onda je jednačina promjene puta (visine) ΔHi
kao na slici 5. Kinematske jednačine promjene visine i brzine rakete tokom
vertikalnog leta daju odnose brzine, ubrzanja, puta i vremena. Ako se zna
ubrzanje u nekom intervalu vremena može se izračunati prmjena brzine u
u tom intervalu,
Δvi = a*Δti .
Ako se zna promjena brzine može se izračunati pređena visina u tom intervalu
ΔHi = Δvi*
Δti/2.
Sabiranjem vremenskih intervala Δti
od početka kretanja do nekog proizvoljnog trenutka u toku leta
dobija se vrijeme leta ti do tog
trenutka. Sabiranjem promjena brzina
Δvi
u svim intervalima do nekog proizvoljnog intrvala i,
dobija se ukupna brzina u trenutku leta ti.
Sabiranjem promjena visine
ΔHi
u svim intervalima do nekog proizvoljnog intrvala i,
dobija se ukupna visina u trenutku leta ti.
Međutim, da bi se određivali pređeni put, brzina i vreijeme leta
potrebno je poznavati ubrzanje a kojem je podvrgnuta
raketa.
Prema Drugom Njutnovom zakonu ubrzanje, promjena brzine i
pravca su posledica dejstva spoljašnjih sila na tijelo, u ovom
slučaju raketu.
 U jednačini su F - rezultantna sila na tijelo u N,
m - masa tijela u kg i a - ubrzanje u m/s2.
Drugi Njutnov zakon može da se napiše i u drugom obliku (slika 6)
U jednačini su F - rezultantna sila na tijelo u N,
m - masa tijela u kg i a - ubrzanje u m/s2.
Drugi Njutnov zakon može da se napiše i u drugom obliku (slika 6)
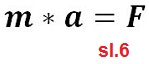 slijedi jednačina (slika 7), u kojoj se ubrzanje prikazuje kao
promjena brzina u intervalu vremena. Suština aproksimacije o
jednako ubrazanom kretanju ovdje je jasno prikazano. Ubrzanje
se mijenja tokom leta, ali u malom intervalu vremena uzima se
njegova srednja vrijednost i tako se može samo u njemu smatrati
konstantnim.
slijedi jednačina (slika 7), u kojoj se ubrzanje prikazuje kao
promjena brzina u intervalu vremena. Suština aproksimacije o
jednako ubrazanom kretanju ovdje je jasno prikazano. Ubrzanje
se mijenja tokom leta, ali u malom intervalu vremena uzima se
njegova srednja vrijednost i tako se može samo u njemu smatrati
konstantnim.
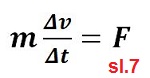 Ovo unosi grešku u proračun. Ukoliko je primijenjeni
interval vremena manji, greška je manja. Praksa je pokazala da se
dovoljna tačnost postiže ako je vremenski inerbal numeričke
integacije 0.001 - 0.01 sec za kretanje u lanseru
i 0.01 - 0.1 za slobodni dio putanje. Sa trenutnim
stanjem računarske tehnike vremenski interval numeričke integracije
može biti i manji, pa se postiže veća tačnost.
Ovo unosi grešku u proračun. Ukoliko je primijenjeni
interval vremena manji, greška je manja. Praksa je pokazala da se
dovoljna tačnost postiže ako je vremenski inerbal numeričke
integacije 0.001 - 0.01 sec za kretanje u lanseru
i 0.01 - 0.1 za slobodni dio putanje. Sa trenutnim
stanjem računarske tehnike vremenski interval numeričke integracije
može biti i manji, pa se postiže veća tačnost.
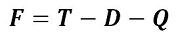 Sila F je rezultanta svih sila koje djeluju na raketu
tokom leta:
sile potiska T, sile otpora D i sile gravitacije Q.
Sila F je rezultanta svih sila koje djeluju na raketu
tokom leta:
sile potiska T, sile otpora D i sile gravitacije Q.
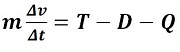 Njutnov zakon sada može da se prikaže u razvijenom obliku:
, a iz nje slijedi formula za promjenu brzine u proizvoljnom
intervalu vremena.
Njutnov zakon sada može da se prikaže u razvijenom obliku:
, a iz nje slijedi formula za promjenu brzine u proizvoljnom
intervalu vremena.
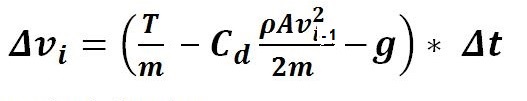
Brzina u proizvoljnom trenutku dobija se dodavanjem promjene
brzine u odgovarajućem intervalu.
Brzina vi-1 je brzina iz prethodne
iteracije.

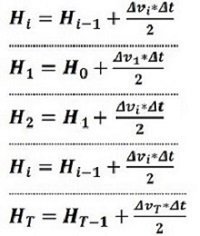
 Za modelarsku raketu to može biti dijagram promjene sile potiska
u funkciji vremena modelarskog raketnog motora B4.
Iz dijagrama sile potiska T = f(t) za
svako zadato vrijeme može se očitati vrijednost sile
T. Masa rakete mR se
mijenja na aktivnom dijelu putanje, zbog sagorijevanja raketnog
goriva. I sila potiska i masa rakete značajno se mijenjaju tokom
vremena. Da bi uticaj tih promjena na vrijednosti proračuna brzine
rakete i pređenog puta bio zanemarljiv, proračuni se vrše za jako
male intervale vremena. Ovakav pristup omogučava da se kretanje
rakete u postavljenom intervalu vremena posmatra kao jednako
ubrzano. Na osnovu jednačina koje važe za pravolinijsko jednako -
ubrzano kretanje mogu se izračunati brzina i put rakete u svakom
intervalu. Njihovim sabiranjem mogu se dobiti parcijalne, ali i
ukupna vrijednost. Ovakav pristup proračunu naziva se numerička
integracija diferencijalnih jednačina.
Za modelarsku raketu to može biti dijagram promjene sile potiska
u funkciji vremena modelarskog raketnog motora B4.
Iz dijagrama sile potiska T = f(t) za
svako zadato vrijeme može se očitati vrijednost sile
T. Masa rakete mR se
mijenja na aktivnom dijelu putanje, zbog sagorijevanja raketnog
goriva. I sila potiska i masa rakete značajno se mijenjaju tokom
vremena. Da bi uticaj tih promjena na vrijednosti proračuna brzine
rakete i pređenog puta bio zanemarljiv, proračuni se vrše za jako
male intervale vremena. Ovakav pristup omogučava da se kretanje
rakete u postavljenom intervalu vremena posmatra kao jednako
ubrzano. Na osnovu jednačina koje važe za pravolinijsko jednako -
ubrzano kretanje mogu se izračunati brzina i put rakete u svakom
intervalu. Njihovim sabiranjem mogu se dobiti parcijalne, ali i
ukupna vrijednost. Ovakav pristup proračunu naziva se numerička
integracija diferencijalnih jednačina.
 Bilo da leti modelarska raketa bilo da se lansira raketa za put do
Marsa, principi na kojima se zasniva rad raketa su apsolutno isti. U ranim
danima raketne tehnike, let raketnih naprava bio je nesiguan. Poneka je
letjela tamo đe je usmjerena, ali su mnoge krivudale ili eksplodirale prije
vremena.
Poslije vjekova pokušaja i grešaka, pokazalo se da je stvarni napredak u raketnoj
tehnici zavisio od naučnog razumijevanja kretanja. Do toga je došlo u XVII vijeku,
sa radovima velikih naučnika, Galileo Galileja i Isaka Njutna. Galilej je proučavao
kretanje na strmoj ravni i otkrio zakon inercije (svako tijelo pruža otpor promjenama
u svom kretanju). Isak Njutn je formulisao tri zakona kretanja i
tako otvorio put ka rješavanju problema u raketnoj tehnici, a nju promovisao
u naučnu disciplinu.
Bilo da leti modelarska raketa bilo da se lansira raketa za put do
Marsa, principi na kojima se zasniva rad raketa su apsolutno isti. U ranim
danima raketne tehnike, let raketnih naprava bio je nesiguan. Poneka je
letjela tamo đe je usmjerena, ali su mnoge krivudale ili eksplodirale prije
vremena.
Poslije vjekova pokušaja i grešaka, pokazalo se da je stvarni napredak u raketnoj
tehnici zavisio od naučnog razumijevanja kretanja. Do toga je došlo u XVII vijeku,
sa radovima velikih naučnika, Galileo Galileja i Isaka Njutna. Galilej je proučavao
kretanje na strmoj ravni i otkrio zakon inercije (svako tijelo pruža otpor promjenama
u svom kretanju). Isak Njutn je formulisao tri zakona kretanja i
tako otvorio put ka rješavanju problema u raketnoj tehnici, a nju promovisao
u naučnu disciplinu.
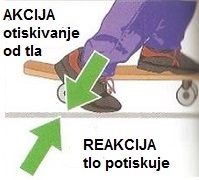 Sila (označava se sa F) je posledica djelovanja jednog
objekta (tijela) na drugi. Ispoljava se kao vučenje, pritisak, guranje.
Jedinica mjere za silu je Njutn (N).
Sile uvijek djeluju u paru, AKCIJA = REAKCIJA. Te dvije sile su jednakae i djeluju
suprotno jedna drugoj. U primjeru na slici dječak se otiskuje nogom od tla. To je
AKCIJA. Tlo potiskuje djećaka. To je REAKCIJA.
Sila (označava se sa F) je posledica djelovanja jednog
objekta (tijela) na drugi. Ispoljava se kao vučenje, pritisak, guranje.
Jedinica mjere za silu je Njutn (N).
Sile uvijek djeluju u paru, AKCIJA = REAKCIJA. Te dvije sile su jednakae i djeluju
suprotno jedna drugoj. U primjeru na slici dječak se otiskuje nogom od tla. To je
AKCIJA. Tlo potiskuje djećaka. To je REAKCIJA.  Balon se kreće sve dok pritisak u njemu ne opadne do pritiska okoline.
Balon se kreće sve dok pritisak u njemu ne opadne do pritiska okoline. 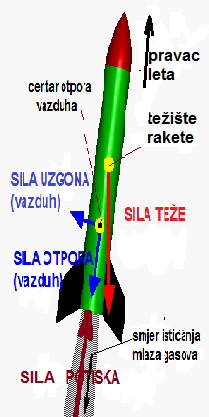 Ta reaktivna sila naziva se SILA POTISKA
raketnog motora, ili prosto POTISAK. Potisak preko motora djeluje na raketu i
prema Drugom Njutnovom zakonu ubrzava je, dajući joj potrebnu brzinu.
Raketni motor ima ograničeno vrijeme sagorijevanja. Kad gorivo u njemu prestane
da gori, POTISAK opada na nulu. Raketa, u skladu sa Prvim Njutnovim zakonom,
nastavlja da se kreće po inerciji, ali ne može beskonačno nastaviti tako . Na nju
tokom leta djeluju sile iz okruženja, SILA TEŽE i OTPOR VAZDUHA. Sila teže i
sila otpora vazduha usporavaju raketu, pa kad dostigne najvisočiju tačku
(tjeme putanje) počinje da pada prema zemlji.
Ta reaktivna sila naziva se SILA POTISKA
raketnog motora, ili prosto POTISAK. Potisak preko motora djeluje na raketu i
prema Drugom Njutnovom zakonu ubrzava je, dajući joj potrebnu brzinu.
Raketni motor ima ograničeno vrijeme sagorijevanja. Kad gorivo u njemu prestane
da gori, POTISAK opada na nulu. Raketa, u skladu sa Prvim Njutnovim zakonom,
nastavlja da se kreće po inerciji, ali ne može beskonačno nastaviti tako . Na nju
tokom leta djeluju sile iz okruženja, SILA TEŽE i OTPOR VAZDUHA. Sila teže i
sila otpora vazduha usporavaju raketu, pa kad dostigne najvisočiju tačku
(tjeme putanje) počinje da pada prema zemlji.





 Ako su od balze, onda vlakna drveta moraju biti poprečna u odnosu na
rakete. Krilca se postavljaju paralelno uzdužnoj osi rakete, okomita u
odnosu na tijelo. Ivica krilca prema vrhu rakete naziva se napadna jer
dočekuje struju vazduha. Izlazna ivica je okrenuta ka zadnjem kraju.
Sa nje vazdušna struja napušta krilce. Dodirna ivica sa tijelom se naziva
korijen krilca. Spoj krilca i tijela kod modelarskih raketa izvodi se
lijepljenjem i mora biti jak, da ne bi došlo do otpadanja.
Ako su od balze, onda vlakna drveta moraju biti poprečna u odnosu na
rakete. Krilca se postavljaju paralelno uzdužnoj osi rakete, okomita u
odnosu na tijelo. Ivica krilca prema vrhu rakete naziva se napadna jer
dočekuje struju vazduha. Izlazna ivica je okrenuta ka zadnjem kraju.
Sa nje vazdušna struja napušta krilce. Dodirna ivica sa tijelom se naziva
korijen krilca. Spoj krilca i tijela kod modelarskih raketa izvodi se
lijepljenjem i mora biti jak, da ne bi došlo do otpadanja.
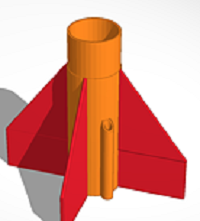 Stabilizator je skup krilaca, učvršćenih na tijelu rakete. Stabilizator
obično ima 4 , a u konstrukcijama modelarskih raketa srijeću se
stabilizatori i sa tri krilca. Površina krilaca, raspon krilaca, broj i položaj
krilaca su faktori koji utiču na stabilnost leta modelarske rakete. Vazdušni
otpor strujanja oko stabilizatora ima značajan udio u ukupnom otporu kojeg
stvara raketa. Zato se traži optimum između dimenzija krilaca
i najbolje stabilnosti leta rakete.
Stabilizator je skup krilaca, učvršćenih na tijelu rakete. Stabilizator
obično ima 4 , a u konstrukcijama modelarskih raketa srijeću se
stabilizatori i sa tri krilca. Površina krilaca, raspon krilaca, broj i položaj
krilaca su faktori koji utiču na stabilnost leta modelarske rakete. Vazdušni
otpor strujanja oko stabilizatora ima značajan udio u ukupnom otporu kojeg
stvara raketa. Zato se traži optimum između dimenzija krilaca
i najbolje stabilnosti leta rakete.
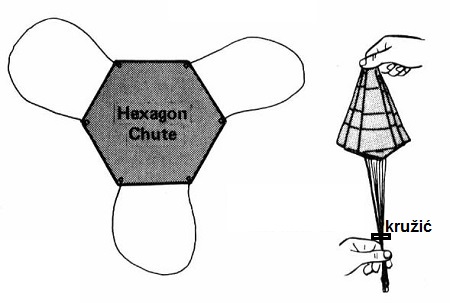
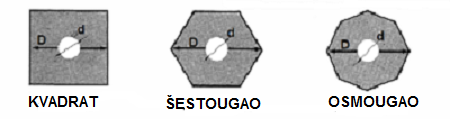 Padobran se pravi od plastične folije. Praktičan za primjenu u modelarskim raketama
je šestougaoni oblik (dobro otvaranje, nema zamršivanja konaca, lak za pakovanje).
Što je površina padobrana veća, komplet rakete sa motorom i kapom, spušta se
laganije. Velika površina traži veći prostor za pakovanje u tijelu rakete. Konstruktor
nalazi optimum između ova dva oprečna zahtjeva. U sredini površine padobrana je mali
otvor (prećnik d). On sprječava ljujlanje padobrana tokom spuštanja. Ljuljanje padobrana
izaziva neravnomjernu brzinu propadanja, pa ga treba izbjeći.
Padobran se pravi od plastične folije. Praktičan za primjenu u modelarskim raketama
je šestougaoni oblik (dobro otvaranje, nema zamršivanja konaca, lak za pakovanje).
Što je površina padobrana veća, komplet rakete sa motorom i kapom, spušta se
laganije. Velika površina traži veći prostor za pakovanje u tijelu rakete. Konstruktor
nalazi optimum između ova dva oprečna zahtjeva. U sredini površine padobrana je mali
otvor (prećnik d). On sprječava ljujlanje padobrana tokom spuštanja. Ljuljanje padobrana
izaziva neravnomjernu brzinu propadanja, pa ga treba izbjeći.
 Konci oblikuju kupolu i veza su padobrana sa ostalim djelovima rakete. Protežu
se iz svakog ugla kupole i vezuju u centralni čvor. Osim konaca u spoju
padobrana sa raketom koriste se ribarsko vrtilo (sprečava uvrtanje konaca) i
elastična gumica (za ublažavanje šoka otvaranja).
Padobran se u svemirskim istraživanjim koristi u odgovornim i vrlo
teškim okolnostima, kao što je spuštanje svemirskih letilica na Zemlju,
što pokazuje koliko je važan sklop za letilice. Modelarske rakete daju priliku
da se njegova funkcija i izrada detaljno prouče kroz eksperiment.
Konci oblikuju kupolu i veza su padobrana sa ostalim djelovima rakete. Protežu
se iz svakog ugla kupole i vezuju u centralni čvor. Osim konaca u spoju
padobrana sa raketom koriste se ribarsko vrtilo (sprečava uvrtanje konaca) i
elastična gumica (za ublažavanje šoka otvaranja).
Padobran se u svemirskim istraživanjim koristi u odgovornim i vrlo
teškim okolnostima, kao što je spuštanje svemirskih letilica na Zemlju,
što pokazuje koliko je važan sklop za letilice. Modelarske rakete daju priliku
da se njegova funkcija i izrada detaljno prouče kroz eksperiment.
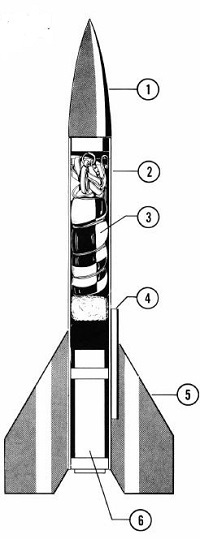
 Modelarski raketni motor daje raketi pogon za let. U njemu gori raketno gorivo
stvarajući visoku temperaturu i pritisak.
Modelar ne pravi motor, nego ga nabavlja od ovlašćenog proizvođača i ugrađuje
u modelarsku raketu gotovog. Spolja se uočava papirna obloga koja formira
komoru motora, objedinjavajući mlaznik, raketno gorivo i dno(pregrada)
komore. Pregrada (dno) služi da zatvori komoru, tako da barutni gasovi
ističu samo kroz mlaznik. Dno komore u slučaju modelarskih motora je
presovana usporačka smješa koja se pripaljuje od gorenja baruta i
poslije izvjesnog vremena (4-6 sec) izbacuje padobran.
Spoljni prečnici standardnih motora su 12 do 18 mm, a dužine su 50
do 100 mm. Konstrukcija modelarskog raketnog motora i teorijska osnova
rada raketnih motora su posebno, opširno poglavlje u okviru kursa o
modelarskim raketnim motorima.
Modelarski raketni motor daje raketi pogon za let. U njemu gori raketno gorivo
stvarajući visoku temperaturu i pritisak.
Modelar ne pravi motor, nego ga nabavlja od ovlašćenog proizvođača i ugrađuje
u modelarsku raketu gotovog. Spolja se uočava papirna obloga koja formira
komoru motora, objedinjavajući mlaznik, raketno gorivo i dno(pregrada)
komore. Pregrada (dno) služi da zatvori komoru, tako da barutni gasovi
ističu samo kroz mlaznik. Dno komore u slučaju modelarskih motora je
presovana usporačka smješa koja se pripaljuje od gorenja baruta i
poslije izvjesnog vremena (4-6 sec) izbacuje padobran.
Spoljni prečnici standardnih motora su 12 do 18 mm, a dužine su 50
do 100 mm. Konstrukcija modelarskog raketnog motora i teorijska osnova
rada raketnih motora su posebno, opširno poglavlje u okviru kursa o
modelarskim raketnim motorima.
 Električna pripala se koristi za aktivianje modelarskih raketnih motora.
Modelar ih ne pravi, nego nabavlja. Obično su u kompletu sa modelarskim
raketnim motorima, ali se mogu dobiti i posebno. Električna pripala čine
dva tanka (0.5mm) bakarna provodnika koji su spojeni mostom od tankog
elekrootpornog provodnika, prečnika d=0.10mm, dužine l=6.00mm, omskog
otpora 0.6Ω (ohm). Na vrh pripale, u dužini otpornika, nanijeta je
zapaljiva pirotehnička smješa. Kad se slobodni krajevi provodnika pripale
spoje na izvor struje (baterija 4.5V) most pripale se usija (700 ℃),
upali pirotehničku smješu. Plamen pirotehničke smješe pali blok raketnog
goriva, stvaraju se produkti sagorijevanja, ističu kroz mlaznik. Taj
proces naziva se aktiviranjem (inicijacijom) raketnog motora.
Električna pripala se koristi za aktivianje modelarskih raketnih motora.
Modelar ih ne pravi, nego nabavlja. Obično su u kompletu sa modelarskim
raketnim motorima, ali se mogu dobiti i posebno. Električna pripala čine
dva tanka (0.5mm) bakarna provodnika koji su spojeni mostom od tankog
elekrootpornog provodnika, prečnika d=0.10mm, dužine l=6.00mm, omskog
otpora 0.6Ω (ohm). Na vrh pripale, u dužini otpornika, nanijeta je
zapaljiva pirotehnička smješa. Kad se slobodni krajevi provodnika pripale
spoje na izvor struje (baterija 4.5V) most pripale se usija (700 ℃),
upali pirotehničku smješu. Plamen pirotehničke smješe pali blok raketnog
goriva, stvaraju se produkti sagorijevanja, ističu kroz mlaznik. Taj
proces naziva se aktiviranjem (inicijacijom) raketnog motora.
 Nema mnogo djelova ni materijala potrebnih za izradu modelarskih raketa. Nijesu
ni skupi, a dostupni su. Kad se prikupe i sastave svi djelovi, pa ako se to
lijepo dekoriše, dobija se sklop sličan kao na slici desno. Svi djelovi mogu
da se nabave gotovi, pojedinačno ili kao komplet modelarske rakete. Tada se
oni samo sastavljaju. Međutim, sve djelove osim motora i pripale modelar može i
sam da napravi: tijelo, kapu, krilca, padobran, vođice. Obično tako rade iskusniji
modelari praveći specijalne konstrukcije takmičarskih raketa ili maketa poznatih
rješenja u raketnoj tehnici:Apolo itd. Lansiranje modelarske rakete predstavlja
i za kreatore rakete i za sve prisutne izuzetan doživljaj i iskustvo.
Nema mnogo djelova ni materijala potrebnih za izradu modelarskih raketa. Nijesu
ni skupi, a dostupni su. Kad se prikupe i sastave svi djelovi, pa ako se to
lijepo dekoriše, dobija se sklop sličan kao na slici desno. Svi djelovi mogu
da se nabave gotovi, pojedinačno ili kao komplet modelarske rakete. Tada se
oni samo sastavljaju. Međutim, sve djelove osim motora i pripale modelar može i
sam da napravi: tijelo, kapu, krilca, padobran, vođice. Obično tako rade iskusniji
modelari praveći specijalne konstrukcije takmičarskih raketa ili maketa poznatih
rješenja u raketnoj tehnici:Apolo itd. Lansiranje modelarske rakete predstavlja
i za kreatore rakete i za sve prisutne izuzetan doživljaj i iskustvo.
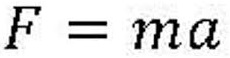 Da raketa krene sa zemlje i dobije brzinu, na nju mora da djeluje sila,
SILA POTISKA. RAKETNI MOTOR ima ulogu da stvara SILU POTISKA.
Odnos sile potiska motora, težine rakete i ubrzanja rakete dat je Drugim
Njutnovim zakonom (slika desno, F - sila potiska, m - masa rakete, a - ubrzanje).
Ako se smatra da je kretanje rakete u toku rada raketnog motora pravolinijsko jednako ubrzano
onda brzina i ubrzanje imaju relaciju
Da raketa krene sa zemlje i dobije brzinu, na nju mora da djeluje sila,
SILA POTISKA. RAKETNI MOTOR ima ulogu da stvara SILU POTISKA.
Odnos sile potiska motora, težine rakete i ubrzanja rakete dat je Drugim
Njutnovim zakonom (slika desno, F - sila potiska, m - masa rakete, a - ubrzanje).
Ako se smatra da je kretanje rakete u toku rada raketnog motora pravolinijsko jednako ubrzano
onda brzina i ubrzanje imaju relaciju
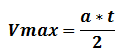 (slika desno, t je vrijeme rada raketnog motora)
Kako je masa konstrukcije
poznata, brzina rakete se određuje na osnovu zadatog dometa, jasno je
da Drugi Njutonov zakon omogućava procjenu potrebne sile potiska raketnog
motora. Na osnovu vrijednosti sile potiska mogu se odrediti svi ostali pogonski
parametri raketnog motora (količina goriva, vrsta goriva, vrijeme rada, pritisak,
temperatura itd). Vrijeme rada raketnog motora je ograničeno (nekoliko minuta).
Dio putanje koji raketa pređe dok je motor aktivan, naziva se aktivni dio putanje.
Kad motor prestane da radi, na raketu ne djeluju pogonske sile. Tu počinje
pasivni dio putanje na kojem , prema Prvom Njutnovom zakonu, ona nastavlja da se
kreće po inerciji.
(slika desno, t je vrijeme rada raketnog motora)
Kako je masa konstrukcije
poznata, brzina rakete se određuje na osnovu zadatog dometa, jasno je
da Drugi Njutonov zakon omogućava procjenu potrebne sile potiska raketnog
motora. Na osnovu vrijednosti sile potiska mogu se odrediti svi ostali pogonski
parametri raketnog motora (količina goriva, vrsta goriva, vrijeme rada, pritisak,
temperatura itd). Vrijeme rada raketnog motora je ograničeno (nekoliko minuta).
Dio putanje koji raketa pređe dok je motor aktivan, naziva se aktivni dio putanje.
Kad motor prestane da radi, na raketu ne djeluju pogonske sile. Tu počinje
pasivni dio putanje na kojem , prema Prvom Njutnovom zakonu, ona nastavlja da se
kreće po inerciji. 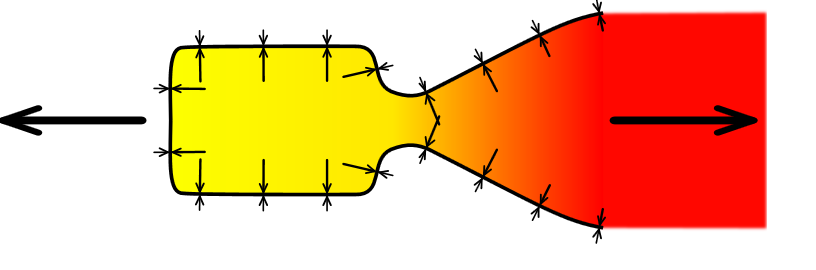 Jedna strane omotača komore je potpuno zatvorena. Dio koji zatvara komoru naziva
se pregrada (dno komore). Suprotno od pregrade komoru ograničava dio sa otvorom.
To je mlaznik. Kroz mlaznik iz komore, izložena pritisku, ističe gasna masa visoke
temperature. Uzdužni profil mlaznika ima specijaln oblik. Specijalni profil se
naziva De Laval-ova mlaznica. Sa strane komore profil se sužava.
To je konvergentna (sužavajuća) sekcija mlaznika.
Jedna strane omotača komore je potpuno zatvorena. Dio koji zatvara komoru naziva
se pregrada (dno komore). Suprotno od pregrade komoru ograničava dio sa otvorom.
To je mlaznik. Kroz mlaznik iz komore, izložena pritisku, ističe gasna masa visoke
temperature. Uzdužni profil mlaznika ima specijaln oblik. Specijalni profil se
naziva De Laval-ova mlaznica. Sa strane komore profil se sužava.
To je konvergentna (sužavajuća) sekcija mlaznika.
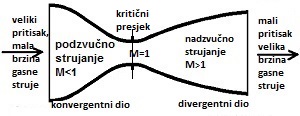
 U njoj se pritisak gasa iz komore smanjuje, a brzina strujanja povećava. Uobičajeno
je u mlaznoj propulziji da se brzina strujanja gasa prikazuje Mahovim brojem.
Mahov broj M je odnos brzine struje gasa V i
brzine prostiranja zvuka kroz vazduh c, M = V/c . U konvergentnoj
sekcijij Mahov broj je manji od 1 (M < 1). Brzina struje gasa
se povećava sužavanjem profila, ali samo do nekog presjeka. Pokazalo se da je
u tom presjeku Mahov broj jednak jedinici, M = 1 i da se daljim
sužavanjem profila brzina strujanja ne povećava.
Presjek De Laval-ovog mlaznika, u kojem je M = 1, a poslije kojeg
ne dolazi do povećanja brzine strujanja, naziva se kritični presjek.
To je ujedno i najmanji presjek mlaznika, jer su istraživanja pokazala da se brzina
strujanja gasa u mlaznici povećava samo povećanjem presjeka profila. Tako nastaje
divergentna sekcija De Laval-ovog mlaznika. U njoj je Mahov broj veći od jedinice,
M > 1 . . Ovakav profil mlaznika omogućava da gasna masa na izlazu
dostigne nadzvučne brzine toka, M = 5-8 (1800 do 2800 m/sec ).
U njoj se pritisak gasa iz komore smanjuje, a brzina strujanja povećava. Uobičajeno
je u mlaznoj propulziji da se brzina strujanja gasa prikazuje Mahovim brojem.
Mahov broj M je odnos brzine struje gasa V i
brzine prostiranja zvuka kroz vazduh c, M = V/c . U konvergentnoj
sekcijij Mahov broj je manji od 1 (M < 1). Brzina struje gasa
se povećava sužavanjem profila, ali samo do nekog presjeka. Pokazalo se da je
u tom presjeku Mahov broj jednak jedinici, M = 1 i da se daljim
sužavanjem profila brzina strujanja ne povećava.
Presjek De Laval-ovog mlaznika, u kojem je M = 1, a poslije kojeg
ne dolazi do povećanja brzine strujanja, naziva se kritični presjek.
To je ujedno i najmanji presjek mlaznika, jer su istraživanja pokazala da se brzina
strujanja gasa u mlaznici povećava samo povećanjem presjeka profila. Tako nastaje
divergentna sekcija De Laval-ovog mlaznika. U njoj je Mahov broj veći od jedinice,
M > 1 . . Ovakav profil mlaznika omogućava da gasna masa na izlazu
dostigne nadzvučne brzine toka, M = 5-8 (1800 do 2800 m/sec ).
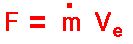 Značaj ovih vrijednosti brzine strujanja gasa iz raketnog motora je vidljiv kad
se analizira jednačina sile potiska motora. Prema
Trećem Njutonovom zakonu (REAKCIJA = - AKCIJA)
sila potiska je proizvod iz protoka (prolaz mase u jedinici vremena) gasne mase
i brzine strujanja gasa na izlaznom presjeku iz mlaznice. Što je brzina isticanja
veća, veća je sila potiska. Veća sila potiska, pri istim ostalim parametrima,
znači ili više korisnog tereta u raketi ili veći domet rakete. De Laval-ov
mlaznik je sjajan primjer, kako se analizom procesa dostiže maksimalni koeficijent
iskoristivosti toplotne mašine.
Značaj ovih vrijednosti brzine strujanja gasa iz raketnog motora je vidljiv kad
se analizira jednačina sile potiska motora. Prema
Trećem Njutonovom zakonu (REAKCIJA = - AKCIJA)
sila potiska je proizvod iz protoka (prolaz mase u jedinici vremena) gasne mase
i brzine strujanja gasa na izlaznom presjeku iz mlaznice. Što je brzina isticanja
veća, veća je sila potiska. Veća sila potiska, pri istim ostalim parametrima,
znači ili više korisnog tereta u raketi ili veći domet rakete. De Laval-ov
mlaznik je sjajan primjer, kako se analizom procesa dostiže maksimalni koeficijent
iskoristivosti toplotne mašine.
 Izrađuju se presovanjem, livenjem, ekstruzijom. Presovanje se primjenjuje samo u
slučaju veoma malih barutnih blokova (za modelarske raketne motore).
Izrađuju se presovanjem, livenjem, ekstruzijom. Presovanje se primjenjuje samo u
slučaju veoma malih barutnih blokova (za modelarske raketne motore).
 Ekstruzija je pogodan i produktivan način izrade barutnih zrna, ali njena primjena
je ograničena na prečnike barutnih blokova do 200 mm. Livenjem se
mogu dobiti barutni blokovi svih veličina, od najmanjih (za modelarske raketne
motore) do najvećih za svemirske rakete. Pogonsko gorivo za jedan buster motor
Spejs Šatla (Space Shuttle Solid Rocket Boosters) je teško oko 500.000,00 kg,
a ukupna težina motora je oko 591.000,00 kg. Tako veliki barutni blok nije mogao
da se dobije ni livenjem. Liveni su segmenti manje težine i onda se spajali u
cjelinu zahtijevanu konstrukcijom Space Šatla.
Poređenja radi, modelarski raketni motor sadrži 5 grama raketnog goriva,
motor protivgradne rakete TG-10 1500 grama. Principi rada motora su u svim
slučajevima isti i ne zavise od količine pogonskog punjenja.
Da bi se ostvario raketni pogon (sila potiska) potrebna je za svaki raketni
motor određena količina gasne mase. Čvrsto raketno gorivo gasnu masu daje
sagorijevanjem. Raketno gorivo treba da sagorijeva postepeno. Brzina gorenja
gorenja je jedan od parametara čvrstog raketnog goriva koji utiče na stvaranje
gasne mase. Veća brzina sagorijevanja stvara veću količina gasa u jedinici
vremena. Veća količina gasa u jedinici vremena,veći je pritisak u komori i
veća je sila potiska. Brzina gorenja utiče i na vrijeme sagorijevanja. Veća
brzina gorenja, kraće vrijeme rada raketnog motora. Drugi parametar je oblik
površine sagorijevanja, a treći je put koji treba da prođe front plamena da bi
sav raketni barut izgorio.
Ekstruzija je pogodan i produktivan način izrade barutnih zrna, ali njena primjena
je ograničena na prečnike barutnih blokova do 200 mm. Livenjem se
mogu dobiti barutni blokovi svih veličina, od najmanjih (za modelarske raketne
motore) do najvećih za svemirske rakete. Pogonsko gorivo za jedan buster motor
Spejs Šatla (Space Shuttle Solid Rocket Boosters) je teško oko 500.000,00 kg,
a ukupna težina motora je oko 591.000,00 kg. Tako veliki barutni blok nije mogao
da se dobije ni livenjem. Liveni su segmenti manje težine i onda se spajali u
cjelinu zahtijevanu konstrukcijom Space Šatla.
Poređenja radi, modelarski raketni motor sadrži 5 grama raketnog goriva,
motor protivgradne rakete TG-10 1500 grama. Principi rada motora su u svim
slučajevima isti i ne zavise od količine pogonskog punjenja.
Da bi se ostvario raketni pogon (sila potiska) potrebna je za svaki raketni
motor određena količina gasne mase. Čvrsto raketno gorivo gasnu masu daje
sagorijevanjem. Raketno gorivo treba da sagorijeva postepeno. Brzina gorenja
gorenja je jedan od parametara čvrstog raketnog goriva koji utiče na stvaranje
gasne mase. Veća brzina sagorijevanja stvara veću količina gasa u jedinici
vremena. Veća količina gasa u jedinici vremena,veći je pritisak u komori i
veća je sila potiska. Brzina gorenja utiče i na vrijeme sagorijevanja. Veća
brzina gorenja, kraće vrijeme rada raketnog motora. Drugi parametar je oblik
površine sagorijevanja, a treći je put koji treba da prođe front plamena da bi
sav raketni barut izgorio.
 Treći parametar naziva se debljinom zida (svoda) barutnog bloka i takođe određuje
vrijeme rada raketnog motora. Veća debljina zida barutnog bloka, duže vrijeme rada
motora. Barutni blokovi obično sagorijevaju (najčešće) iz unutrašnjeg kanala prema
spoljnjoj površini bloka. Spoljnja površina bloka je obložena termoizolacionom materijom.
Sa te strane se sprječava gorenje, pa se sagorijevanje odvija samo sa površine unutrašnjeg
kanala. Početna površina sagorijevanja izračunava se kao proizvod dužine konture
profila unutrašnjeg kanala (l) i dužine barutnog bloka L. Barutni blok je spolja
cilindričnog oblika (najčešće). Smjer gorenja je upravan na površinu sagorijevanja,
a sagorijevanje se odvija u paralelnim slojevima, od unutrašnje pa sve do spoljnje
površine barutnog bloka. Postupnim sagorijevanjem svakog sloja goriva stvara
se gasna masa. Kako je zapremina komore ograničena pritisak gasa u njoj raste,
jer je priliv gasne mase od sagorijevanja veći nego što mlaznik dozvoljava isticanje.
Isticanje kroz mlaznik obezbjeđuje da pritisak gasa u komori ne pređe granicu koja bi
dovela do eksplozije.
Veća površina sagorijevanja i veća brzina gorenja daju veći priliv mase gasnih
produkata u komori. Kombinacijom ova dva parametra i deblljine svoda raketnog
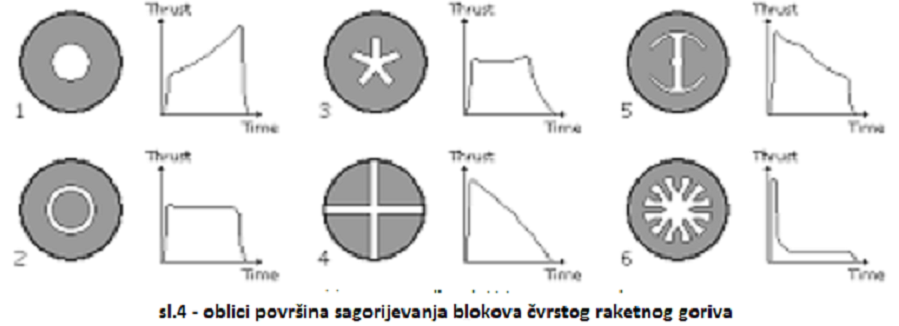
bloka, omogućava se regulacija režima rada motora. Na slici 4 prikazani su
dijagrami promjene sile potiska u funkciji vremena za razne oblike konture
unutrašnjeg kanala barutnog bloka. Najčešće se traži da sila potiska bude
konstantne vrijednosti tokom rada motora (dijagrami 2 i 3 na slici 4) de
konstantne vrijednosti tokom rada motora (dijagrami 2 i 3 na slici 4)
Treći parametar naziva se debljinom zida (svoda) barutnog bloka i takođe određuje
vrijeme rada raketnog motora. Veća debljina zida barutnog bloka, duže vrijeme rada
motora. Barutni blokovi obično sagorijevaju (najčešće) iz unutrašnjeg kanala prema
spoljnjoj površini bloka. Spoljnja površina bloka je obložena termoizolacionom materijom.
Sa te strane se sprječava gorenje, pa se sagorijevanje odvija samo sa površine unutrašnjeg
kanala. Početna površina sagorijevanja izračunava se kao proizvod dužine konture
profila unutrašnjeg kanala (l) i dužine barutnog bloka L. Barutni blok je spolja
cilindričnog oblika (najčešće). Smjer gorenja je upravan na površinu sagorijevanja,
a sagorijevanje se odvija u paralelnim slojevima, od unutrašnje pa sve do spoljnje
površine barutnog bloka. Postupnim sagorijevanjem svakog sloja goriva stvara
se gasna masa. Kako je zapremina komore ograničena pritisak gasa u njoj raste,
jer je priliv gasne mase od sagorijevanja veći nego što mlaznik dozvoljava isticanje.
Isticanje kroz mlaznik obezbjeđuje da pritisak gasa u komori ne pređe granicu koja bi
dovela do eksplozije.
Veća površina sagorijevanja i veća brzina gorenja daju veći priliv mase gasnih
produkata u komori. Kombinacijom ova dva parametra i deblljine svoda raketnog
bloka, omogućava se regulacija režima rada motora. Na slici 4 prikazani su
dijagrami promjene sile potiska u funkciji vremena za razne oblike konture
unutrašnjeg kanala barutnog bloka. Najčešće se traži da sila potiska bude
konstantne vrijednosti tokom rada motora (dijagrami 2 i 3 na slici 4) de
konstantne vrijednosti tokom rada motora (dijagrami 2 i 3 na slici 4)
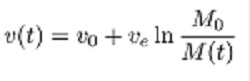
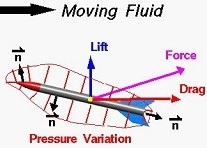
 Aero znači vazduh, a dinamika kretanje. Aerodinamika je dio tehničkih
nauka koji proučava strujanje (kretanje) vazduha oko tijela i dejstva
sila koje tada nastaju. Sile nastale strujanjem vazduha nazivaju se
aerodinamičke sile. Svejedno je da li vazduh struji oko tijela koje
miruje ili se tijelo kreće kroz vazduh koji miruje.
Snažan vjetar obara drveće, skida krovove itd. Aerodinamička sila
nosi avion u letu. Atmosferski vazduh mnogo ometa let raketa. Primjera
radi, modelarska raketa ima težinu 18 grama. Njen motor sadrži 5
grama crnog baruta. Računajući po formuli Ciolkovskog, raketa dobija
maksimalnu brzinu od 209 m/sec. Ako se lansira vertikalno sa tla,
raketa u vazdušnoj atmosferi dositće visinu do 400 metara. Ako bi
bila lansirana u bezvazdušnom prostoru, dostigla bi visinu od oko
2000 metara. Jasno je do otpor vazduha smanjuju domet modelarske
rakete za oko 5 puta. Slično je sa profesionalnim raketama. Otpor
vazduha uzrokuje velike teškoće u konstrukciji i znatne troškove
izrade raketa. Aerodinamika je tu da ukaže na koji način se otpori
vazduha mogu smanjiti na najmanju mjeru. Za to je potrebno mnogo
teoretskog i eksperimentalnog rada.
Aero znači vazduh, a dinamika kretanje. Aerodinamika je dio tehničkih
nauka koji proučava strujanje (kretanje) vazduha oko tijela i dejstva
sila koje tada nastaju. Sile nastale strujanjem vazduha nazivaju se
aerodinamičke sile. Svejedno je da li vazduh struji oko tijela koje
miruje ili se tijelo kreće kroz vazduh koji miruje.
Snažan vjetar obara drveće, skida krovove itd. Aerodinamička sila
nosi avion u letu. Atmosferski vazduh mnogo ometa let raketa. Primjera
radi, modelarska raketa ima težinu 18 grama. Njen motor sadrži 5
grama crnog baruta. Računajući po formuli Ciolkovskog, raketa dobija
maksimalnu brzinu od 209 m/sec. Ako se lansira vertikalno sa tla,
raketa u vazdušnoj atmosferi dositće visinu do 400 metara. Ako bi
bila lansirana u bezvazdušnom prostoru, dostigla bi visinu od oko
2000 metara. Jasno je do otpor vazduha smanjuju domet modelarske
rakete za oko 5 puta. Slično je sa profesionalnim raketama. Otpor
vazduha uzrokuje velike teškoće u konstrukciji i znatne troškove
izrade raketa. Aerodinamika je tu da ukaže na koji način se otpori
vazduha mogu smanjiti na najmanju mjeru. Za to je potrebno mnogo
teoretskog i eksperimentalnog rada.
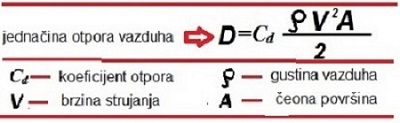
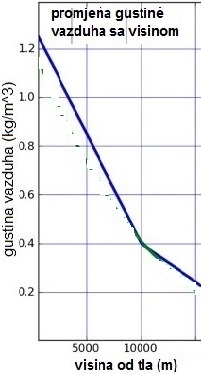 U jednačini se jasno uočava da je sila otpora direktno srazmjerna
gustini vazduha. U nižim slojevima vazdušnog omotača gustina je veća,
i na nivou mora iznosi 1,2 kg/m3. Na 2500 m visine gustina
opada na 1,0 kg/m3, oko 20%. Za toliko je manja i sila
otpora. Smanjenje gustine sa visinom leta je povod za konstrukciju
višestepenih raketa. Prvi stepen iznese raketu do slojeva manje
gustine, saopšti joj neku brzinu i onda se odvaja. Ostali stepeni,
povećavaju brzinu, ali pošto je gustina manja, sila otpora vazduha je
manja. Višestepena konstrukcija omogućava ekonomičniju konstrukciju
rakete. Vazduh utiče na silu otpora i svojom viskoznošću µ.
Viskoznost je tečljivost fluida (tečnosti i gasova) i utiče na tok njegove struje
dodiru sa površinom rakete. Glatka spoljna površina (manja hrapavost) znatno
smanjuje otpore nastale trenjem struje vazduha preko omotača rakete.
U jednačini se jasno uočava da je sila otpora direktno srazmjerna
gustini vazduha. U nižim slojevima vazdušnog omotača gustina je veća,
i na nivou mora iznosi 1,2 kg/m3. Na 2500 m visine gustina
opada na 1,0 kg/m3, oko 20%. Za toliko je manja i sila
otpora. Smanjenje gustine sa visinom leta je povod za konstrukciju
višestepenih raketa. Prvi stepen iznese raketu do slojeva manje
gustine, saopšti joj neku brzinu i onda se odvaja. Ostali stepeni,
povećavaju brzinu, ali pošto je gustina manja, sila otpora vazduha je
manja. Višestepena konstrukcija omogućava ekonomičniju konstrukciju
rakete. Vazduh utiče na silu otpora i svojom viskoznošću µ.
Viskoznost je tečljivost fluida (tečnosti i gasova) i utiče na tok njegove struje
dodiru sa površinom rakete. Glatka spoljna površina (manja hrapavost) znatno
smanjuje otpore nastale trenjem struje vazduha preko omotača rakete.
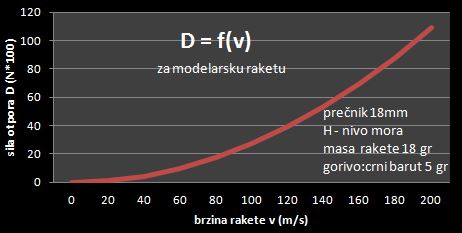 Veličina aeordinamičkih sila najviše zavisi od brzine kretanja
rakete. Ako se brzina poveća za 2, 3, 4 itd puta, sila poraste za 4
9, 16 itd puta, jer je zavisnost kvadratna. Maksimalna brzina
modelarske rakete date na dijagramu iznosi oko 200 m/sec. Pri toj
brzini otpor je 1N (100 gr). Za brzinu od 300 m/sec, otpor bi iznosio
9N (900 grama). Sila potiska modelarskog raketnog motora je 10N (1000grama).
(1000 grama). Kako brzina rakete raste, povećava se i sila otpora kretanju.
Sila otpora D stalno smanjuje brzinu rakete sapštenu od raketnog goriva. Da
bi se ostvarile velike visine raketa, moraju se povećavati brzine raketa.
Zbog otpora vazduha raketni motor mora sadržati velike količine raketnog
goriva da bi se dobila velika brzina. Ako bi se išlo tim putem, morale
bi se praviti ogromne konstrukcije, što je neizvodljivo. Da bi se smanjio
negativan uticaj aerodinamočkih sila optpra, u nižim slojevima atmosfere,
pribjegava se dvostepenim ili trostepenim konstrukcijama raketa.
Veličina aeordinamičkih sila najviše zavisi od brzine kretanja
rakete. Ako se brzina poveća za 2, 3, 4 itd puta, sila poraste za 4
9, 16 itd puta, jer je zavisnost kvadratna. Maksimalna brzina
modelarske rakete date na dijagramu iznosi oko 200 m/sec. Pri toj
brzini otpor je 1N (100 gr). Za brzinu od 300 m/sec, otpor bi iznosio
9N (900 grama). Sila potiska modelarskog raketnog motora je 10N (1000grama).
(1000 grama). Kako brzina rakete raste, povećava se i sila otpora kretanju.
Sila otpora D stalno smanjuje brzinu rakete sapštenu od raketnog goriva. Da
bi se ostvarile velike visine raketa, moraju se povećavati brzine raketa.
Zbog otpora vazduha raketni motor mora sadržati velike količine raketnog
goriva da bi se dobila velika brzina. Ako bi se išlo tim putem, morale
bi se praviti ogromne konstrukcije, što je neizvodljivo. Da bi se smanjio
negativan uticaj aerodinamočkih sila optpra, u nižim slojevima atmosfere,
pribjegava se dvostepenim ili trostepenim konstrukcijama raketa.
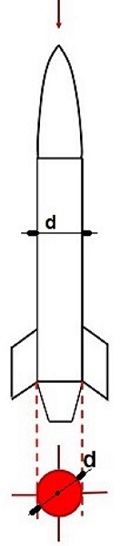 Veličina rakete na silu otpora vazduha utiče preko čeone
površine i dužine. Dužina povećava silu otpora tako što
povećva površinu omotača i time trenje vazdušne struje o
tijelo rakete.
Veličina rakete na silu otpora vazduha utiče preko čeone
površine i dužine. Dužina povećava silu otpora tako što
povećva površinu omotača i time trenje vazdušne struje o
tijelo rakete.
 Duža rakete L, veći omotač, veće trenje,
veća sila otpora. Iz jednačine sile otpora rakete vidi se
da je sila otpora direktno proporcionalna čeonoj površini
rakete. Čeona površina je površina projekcije rakete gledano
u pravcu strujanja vazduha (od vrha rakete).
Rakete su cilindrične površine, pri čemu tijelo rakete ima
najveći prećnik d. Ćeona površina je onda
A = d2π/2 + 4*a*b(četiri projekcije čeonih
površina krilaca).
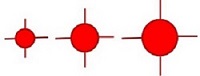
Sila otpora raste sa kvadratom prečnika tijela rakete. Dva, tri,
četiri itd puta veća čeona površina 4,9,16 itd puta veća sila
otpora. Prečnik cilindričnog tijela rakete često se naziva i
kalibar rakete. Kalibar rakete se bira prema dimenzijama korisnog
tereta kojeg raketa nosi i prema prečniku komore raketnog
motora koji nosi raketu. Sila otpora vazduha je faktor sa kojim
se mora uskladiti optimalna konstrukcija rakete. Uticaj čeone
površine na aerodinamičke sile otpora dat je na dijagramu slika 3.
Duža rakete L, veći omotač, veće trenje,
veća sila otpora. Iz jednačine sile otpora rakete vidi se
da je sila otpora direktno proporcionalna čeonoj površini
rakete. Čeona površina je površina projekcije rakete gledano
u pravcu strujanja vazduha (od vrha rakete).
Rakete su cilindrične površine, pri čemu tijelo rakete ima
najveći prećnik d. Ćeona površina je onda
A = d2π/2 + 4*a*b(četiri projekcije čeonih
površina krilaca).
Sila otpora raste sa kvadratom prečnika tijela rakete. Dva, tri,
četiri itd puta veća čeona površina 4,9,16 itd puta veća sila
otpora. Prečnik cilindričnog tijela rakete često se naziva i
kalibar rakete. Kalibar rakete se bira prema dimenzijama korisnog
tereta kojeg raketa nosi i prema prečniku komore raketnog
motora koji nosi raketu. Sila otpora vazduha je faktor sa kojim
se mora uskladiti optimalna konstrukcija rakete. Uticaj čeone
površine na aerodinamičke sile otpora dat je na dijagramu slika 3.
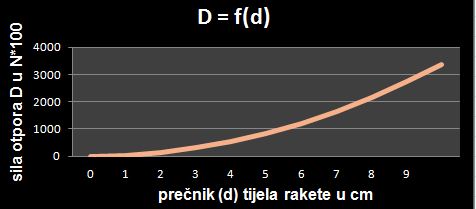 I površina čeonog presjeka je ograničavajući faktor u projektovanju
rakete. I u ovom slučaju rješenje se nalazi u višestepenim raketama.
Buster motori (prvi stepen) pripadaju dijelu rakete sa većim
prečnikom, drugi stepen, ima nešto manji prečnik, a treći stepen
je najmanjeg prečnika u konstukciji rakete.
I površina čeonog presjeka je ograničavajući faktor u projektovanju
rakete. I u ovom slučaju rješenje se nalazi u višestepenim raketama.
Buster motori (prvi stepen) pripadaju dijelu rakete sa većim
prečnikom, drugi stepen, ima nešto manji prečnik, a treći stepen
je najmanjeg prečnika u konstukciji rakete.
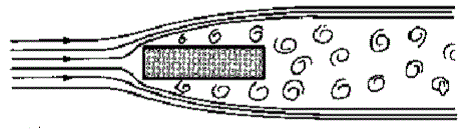 Ako bi se zaoblio čeoni dio tijela, a suzio repni dio,
odvajanje strujnica pomjera se unazad, a vrtloženje počinje
kasnije u odnosu na cilindrični oblik tijela. Sila otpora
vazduha se smanjuje.
Ako bi se zaoblio čeoni dio tijela, a suzio repni dio,
odvajanje strujnica pomjera se unazad, a vrtloženje počinje
kasnije u odnosu na cilindrični oblik tijela. Sila otpora
vazduha se smanjuje.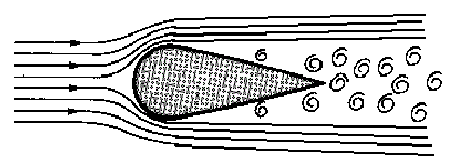 Oblik rakete značajno utiče na veličinu sile otpora. Strujanje
oko dobrog aerodinamičkog profila naziva se laminarno. Strujnice su
pravilno raspoređene oko profila, nema odvajanja. Sila otpora je
svedena na najmanju moguću mjeru u odnosu na sve ostale oblike.
Oblik rakete značajno utiče na veličinu sile otpora. Strujanje
oko dobrog aerodinamičkog profila naziva se laminarno. Strujnice su
pravilno raspoređene oko profila, nema odvajanja. Sila otpora je
svedena na najmanju moguću mjeru u odnosu na sve ostale oblike.
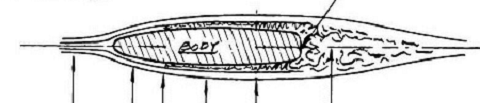
 Istraživanja Njemačkog naučnika Wunibald Kamm-a iz 1930 godine,
pokazala su da najbolja kontura treba da ima čeoni lučni dio
izdužen i da blago prelazi na ciilindar. Cilindara se nastavlja
sužavanjem profila i naglo se prekida ravnom površinom dna konture.
Istraživanja Njemačkog naučnika Wunibald Kamm-a iz 1930 godine,
pokazala su da najbolja kontura treba da ima čeoni lučni dio
izdužen i da blago prelazi na ciilindar. Cilindara se nastavlja
sužavanjem profila i naglo se prekida ravnom površinom dna konture.
 Kada se uzmu u obzir najpovoljniji efekti strujanja vazduha
oko rakete i mogućnosti realne izvodljivosti konstrukcije,
onda se dolazi do zaključka da je najpovoljniji uzdužni profil
rakete kao na slici 5:
Kada se uzmu u obzir najpovoljniji efekti strujanja vazduha
oko rakete i mogućnosti realne izvodljivosti konstrukcije,
onda se dolazi do zaključka da je najpovoljniji uzdužni profil
rakete kao na slici 5:

 Koeficijent sile otpora CCds se ne
izračunava, nema matematičke formule. On se određuje opitima.
Eksperimenti se izvode u aerodinamičkim tunelima u kojima je
model rakete učvršćen, a struja vazduha sa određenom brzinom se
stvara snažnim ventilatorima. Sa razvojem elektronike dobijene su
mogućnosti da se koeficijent otpora određuje i u realnom abijentu
i uslovima tokom leta.
Koeficijent sile otpora CCds se ne
izračunava, nema matematičke formule. On se određuje opitima.
Eksperimenti se izvode u aerodinamičkim tunelima u kojima je
model rakete učvršćen, a struja vazduha sa određenom brzinom se
stvara snažnim ventilatorima. Sa razvojem elektronike dobijene su
mogućnosti da se koeficijent otpora određuje i u realnom abijentu
i uslovima tokom leta.
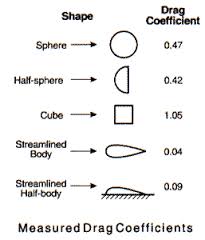 Aerodinamička ispitivanja i određivanje
koeficijenta sile otpora na naučnoj eksperimentalnoj osnovi imaju
tradiciju preko 100 godina. Ta ispitivanja, osim u oblikovanju
raketa, dala su sjajne efekte i u modeliranju automobila i kamiona,
letilica pa čak i bicikala. Zahvaljujući tome postignute su velike
uštede u potrošnji energije, odnosno podizanju efikasnosti objekata
koji se kreću većim brzinama.
Aerodinamička ispitivanja i određivanje
koeficijenta sile otpora na naučnoj eksperimentalnoj osnovi imaju
tradiciju preko 100 godina. Ta ispitivanja, osim u oblikovanju
raketa, dala su sjajne efekte i u modeliranju automobila i kamiona,
letilica pa čak i bicikala. Zahvaljujući tome postignute su velike
uštede u potrošnji energije, odnosno podizanju efikasnosti objekata
koji se kreću većim brzinama.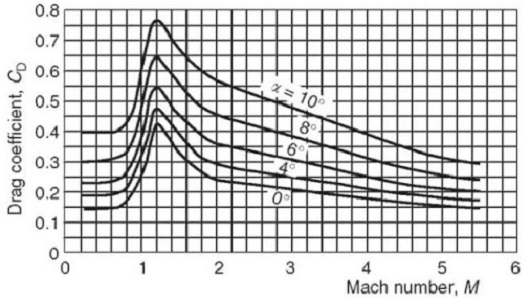
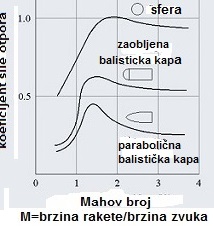 Na priloženim slikama jasno se uočava da koeficijent otpora
Cd zavisi od brzine leta, koja je
ovaj put predstavljena Mahovim brojem. Mahov broj, obilježava se
u aerodinamici i balistici sa Ma, je
odnos brzine leta rakete v i brzine prostiranja
zvuka kroz vazduh a, Ma = v/a.
Mahov broj je veoma pogodan za analizu uticaja brzine na vrijednosti
aerodinamičkih sila zbog svog malog opsega, ali i zbog sadržavanja
uticaja ambijenta, jer se brzina zvuka mijenja sa karakteristikama
vazduha. Primjetan je skok Cd oko
Ma=1 i primjetno je da je vrijednost
Cd veća za Ma > 1.
Brzina zvuka ima vrijednost a = 340 m/s na nivou mora i
temperaturi od 20°.
Na priloženim slikama jasno se uočava da koeficijent otpora
Cd zavisi od brzine leta, koja je
ovaj put predstavljena Mahovim brojem. Mahov broj, obilježava se
u aerodinamici i balistici sa Ma, je
odnos brzine leta rakete v i brzine prostiranja
zvuka kroz vazduh a, Ma = v/a.
Mahov broj je veoma pogodan za analizu uticaja brzine na vrijednosti
aerodinamičkih sila zbog svog malog opsega, ali i zbog sadržavanja
uticaja ambijenta, jer se brzina zvuka mijenja sa karakteristikama
vazduha. Primjetan je skok Cd oko
Ma=1 i primjetno je da je vrijednost
Cd veća za Ma > 1.
Brzina zvuka ima vrijednost a = 340 m/s na nivou mora i
temperaturi od 20°.
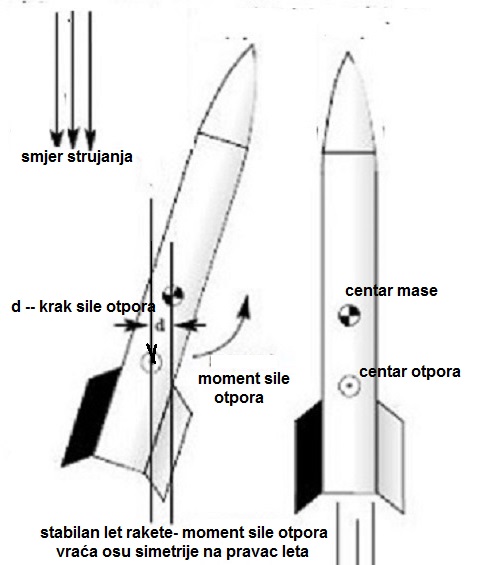


 Što je površina krilaca veća, za stabilizator na kraju rakete,
centar otpora je dalji od vrha. Pomjeranjem stabilizatora unazad
i povećanjem površine njegovih krilaca reguliše se da centar otpora
rakete dođe iza težišta u odnosu na vrh rakete. Rastojanje između
centra otpora i centra mase rakete treba da bude L= 1,5-2 D,
gdje je D prečnik (kalibar) rakete. Položaj centra
otpora i centra mase rakete mogu se odredizno proračunati. Za modelarske
rakete oba centra mogu se lako odrediti, provjeriti i eksperimentalno.
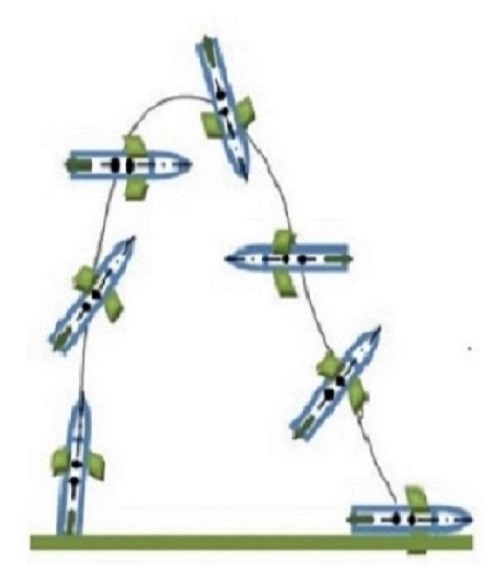
Raketa u letu se ponaša kao "slobodno tijelo" u prostoru. Ako iz
bilo kojeg razloga neka sila, van pravca ose simetrije rakete,
počne da djeluje na raketu izazvaće njenu rotaciju. Rotacija se
uvijek odvija oko težišta (centra gravitacije, centra mase) rakete.
Rotacija tokom leta remeti pravilan let rakete. Ako se ne bi zaustavila,
raketa bi se prevrnula i kretala se po nekontrolisanoj putanji.
Takvo kretanje naziva se nestabilan let, odnosno za raketu se kaže
da je nestabilna.
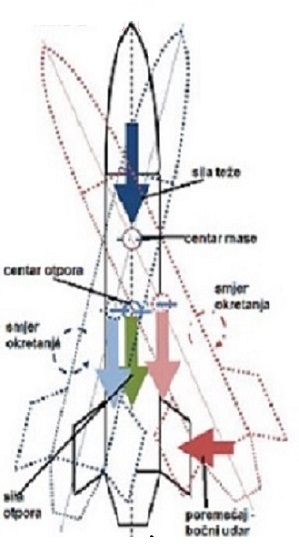
Sile koje stvaraju poremećaj mogu imati različit uzrok. To može
biti udar vjetra, udar od vibracija lansera pri izlijetanju, pojedinačni
dodaci na površini, nepravilna geometrija komponenti rakete
(nesaosnost kape,motora itd). Sve te sile djeluju
tako da okreću raketu oko centra mase (težišta). Da bi se spriječilo
okretanje rakete centar djelovanja aerodinamičkih sila mora se
nalaziti iza centra mase. To se postiže postavljanjem stabilizatora na
repni dio rakete. Stabilizator povećava aerodinamički otpor vazduha,
ali centar njegovog djelovanja pomjera prema donjem kraju rakete,
iza težišta. Zahvaljujući aerodnimaičkim silama stabilizatora raketa
uvijek rotira suprotno poremećaju i vraća se na pravac. Raketa poslije
poremećaja uvijek osciluje oko težišta. Oscilacije se smanjuju uslijed
dejstva stabilizatora i poptuno prestaju. Raketa nastavlja pravilan let
po predviđenoj putanju. Za takvu raketu kaže se da leti stabilno.
Što je površina krilaca veća, za stabilizator na kraju rakete,
centar otpora je dalji od vrha. Pomjeranjem stabilizatora unazad
i povećanjem površine njegovih krilaca reguliše se da centar otpora
rakete dođe iza težišta u odnosu na vrh rakete. Rastojanje između
centra otpora i centra mase rakete treba da bude L= 1,5-2 D,
gdje je D prečnik (kalibar) rakete. Položaj centra
otpora i centra mase rakete mogu se odredizno proračunati. Za modelarske
rakete oba centra mogu se lako odrediti, provjeriti i eksperimentalno.
Raketa u letu se ponaša kao "slobodno tijelo" u prostoru. Ako iz
bilo kojeg razloga neka sila, van pravca ose simetrije rakete,
počne da djeluje na raketu izazvaće njenu rotaciju. Rotacija se
uvijek odvija oko težišta (centra gravitacije, centra mase) rakete.
Rotacija tokom leta remeti pravilan let rakete. Ako se ne bi zaustavila,
raketa bi se prevrnula i kretala se po nekontrolisanoj putanji.
Takvo kretanje naziva se nestabilan let, odnosno za raketu se kaže
da je nestabilna.
Sile koje stvaraju poremećaj mogu imati različit uzrok. To može
biti udar vjetra, udar od vibracija lansera pri izlijetanju, pojedinačni
dodaci na površini, nepravilna geometrija komponenti rakete
(nesaosnost kape,motora itd). Sve te sile djeluju
tako da okreću raketu oko centra mase (težišta). Da bi se spriječilo
okretanje rakete centar djelovanja aerodinamičkih sila mora se
nalaziti iza centra mase. To se postiže postavljanjem stabilizatora na
repni dio rakete. Stabilizator povećava aerodinamički otpor vazduha,
ali centar njegovog djelovanja pomjera prema donjem kraju rakete,
iza težišta. Zahvaljujući aerodnimaičkim silama stabilizatora raketa
uvijek rotira suprotno poremećaju i vraća se na pravac. Raketa poslije
poremećaja uvijek osciluje oko težišta. Oscilacije se smanjuju uslijed
dejstva stabilizatora i poptuno prestaju. Raketa nastavlja pravilan let
po predviđenoj putanju. Za takvu raketu kaže se da leti stabilno.
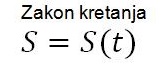

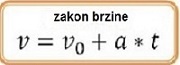 Pravolinijsko kretanje koje ima konstantno ubrzanje a
naziva se jednako ubrzano pravolinijsko kretanje.
Za njega zakon promjene brzine glasi: v = v0 +
a*t.
Ako je poćetna brzina v0=0 jednaka nuli,
onda zakon izgleda v = a*t.
Pravolinijsko kretanje koje ima konstantno ubrzanje a
naziva se jednako ubrzano pravolinijsko kretanje.
Za njega zakon promjene brzine glasi: v = v0 +
a*t.
Ako je poćetna brzina v0=0 jednaka nuli,
onda zakon izgleda v = a*t.
 Jednačina zavisnosti puta od brzine za jednako ubrzano pravolinijsko
kretanje je s = v0*t + a*t2/2.,
a ako je početna brzina jednaka nuli v0=0
zakon pređenog puta glasi s = a*t2/2.
Jednačina zavisnosti puta od brzine za jednako ubrzano pravolinijsko
kretanje je s = v0*t + a*t2/2.,
a ako je početna brzina jednaka nuli v0=0
zakon pređenog puta glasi s = a*t2/2.
 Vertikalni hitac naviše je poseban slučaj jednako ubrzanog
pravolinijskog kretanja tijela u polju sile zemljine teže, sa početnom
brzinom v0 ≥ 0. Ubrzanje vertikalnog
hica jednako je ubrzanju zemljine teže g = 9,81 m/s i
Vertikalni hitac naviše je poseban slučaj jednako ubrzanog
pravolinijskog kretanja tijela u polju sile zemljine teže, sa početnom
brzinom v0 ≥ 0. Ubrzanje vertikalnog
hica jednako je ubrzanju zemljine teže g = 9,81 m/s i
 suprotnog je smjera od brzine, što znači da je smanjuje. Kod
vertikalnog hica naviše ubrzanje uslijed sile gravitacije djeluje
kao usporenje.
suprotnog je smjera od brzine, što znači da je smanjuje. Kod
vertikalnog hica naviše ubrzanje uslijed sile gravitacije djeluje
kao usporenje.
 Tijelo se kreće pod uglom koji se posmatra u ondosu na horizontalni pravac.
Putanja tijela u slučaju kosog hitca je parabola. Odstojanje od koordinatnog
početka do padne tačke je domet XD.
Domet zavisi od početne brzine tijela v0 i od
ugla θ pod kojim hitac startuje(ugao elevacije).
Najviša tačka putanje naziva se tjeme putanje.
Tijelo se kreće pod uglom koji se posmatra u ondosu na horizontalni pravac.
Putanja tijela u slučaju kosog hitca je parabola. Odstojanje od koordinatnog
početka do padne tačke je domet XD.
Domet zavisi od početne brzine tijela v0 i od
ugla θ pod kojim hitac startuje(ugao elevacije).
Najviša tačka putanje naziva se tjeme putanje.
 Odgovor je jednostavan. Uzrok je sila (force). Sila je bilo kakvo
dejstvo koje može učiniti da neko tijelo promijeni svoj oblik ili
kretanje.
Odgovor je jednostavan. Uzrok je sila (force). Sila je bilo kakvo
dejstvo koje može učiniti da neko tijelo promijeni svoj oblik ili
kretanje. Tijelo rakete, vazduh i produkti sagorijevanja barutnog goriva djeluju
uzajamno. Produkti sagorijevanja potiskuju raketu dajući joj brzinu,
težina usporava raketu, a vazduh svojom gustinom stvara aerodinamičku
silu otpora koja takođe usporavaju raketu.
Tijelo rakete, vazduh i produkti sagorijevanja barutnog goriva djeluju
uzajamno. Produkti sagorijevanja potiskuju raketu dajući joj brzinu,
težina usporava raketu, a vazduh svojom gustinom stvara aerodinamičku
silu otpora koja takođe usporavaju raketu.
 Svaka raketa se pravi sa ciljem da da se ostvare postavljeni projektni
zahtjeve. To mogu biti vrsta i količina korisnog tereta, visina
koja se treba dostići itd. U slučaju modelarske rakete projektni
zahtjevi su pravilan let i usporeno spuštanje na tlo. Modelarska
raketa zbog toga ima ima dobro projektovan stabilizator i padobran
kao korisni teret za bezbjedno spuštanje modela na tlo.
Realizaicja projekta rakete odvija se u nekoliko koraka.
Svaka raketa se pravi sa ciljem da da se ostvare postavljeni projektni
zahtjeve. To mogu biti vrsta i količina korisnog tereta, visina
koja se treba dostići itd. U slučaju modelarske rakete projektni
zahtjevi su pravilan let i usporeno spuštanje na tlo. Modelarska
raketa zbog toga ima ima dobro projektovan stabilizator i padobran
kao korisni teret za bezbjedno spuštanje modela na tlo.
Realizaicja projekta rakete odvija se u nekoliko koraka.
 U kretanju rakete razlikuju se tri faze:
kretanje kroz lanserni uređaj,
aktivni dio puta, i pasivni dio puta.
Pod aktivnim dijelom puta podrazumijeva se dio putanje na kojoj radi raketni
motor (dio puta na kojem sagorijeva raketno gorivo). Jedan dio aktivne
putanje obuhvata i kretanje rakete kroz lansirni uređaj. To je neslobodno,
vođeno kretanje.
Drugi dio aktivne putanje odvija se van lansera. To je slobodno
aktivno kretanje. Na aktivnom dijelu putanje raketa dobija ubrzanje pod
dejstvom sile potiska T raketnog motora.
Raketa mora napuštiti lanser sa brzinom koja je dovoljna za stabilan let
na nevođenom dijelu aktivnog puta. Brzina napuštanja lansera se naziva
početna brzina i označava sa v0.. Vrijednost
početne brzine zavisi od ubrzanja rakete a. Na osnovu
početne brzine određuje se dužina lansera. Preporuka je da raketa ima
ubrzanje a ≥ 15 m/s2 da bi bila stabilna
po izlasku iz lansera.
U kretanju rakete razlikuju se tri faze:
kretanje kroz lanserni uređaj,
aktivni dio puta, i pasivni dio puta.
Pod aktivnim dijelom puta podrazumijeva se dio putanje na kojoj radi raketni
motor (dio puta na kojem sagorijeva raketno gorivo). Jedan dio aktivne
putanje obuhvata i kretanje rakete kroz lansirni uređaj. To je neslobodno,
vođeno kretanje.
Drugi dio aktivne putanje odvija se van lansera. To je slobodno
aktivno kretanje. Na aktivnom dijelu putanje raketa dobija ubrzanje pod
dejstvom sile potiska T raketnog motora.
Raketa mora napuštiti lanser sa brzinom koja je dovoljna za stabilan let
na nevođenom dijelu aktivnog puta. Brzina napuštanja lansera se naziva
početna brzina i označava sa v0.. Vrijednost
početne brzine zavisi od ubrzanja rakete a. Na osnovu
početne brzine određuje se dužina lansera. Preporuka je da raketa ima
ubrzanje a ≥ 15 m/s2 da bi bila stabilna
po izlasku iz lansera. 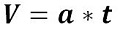
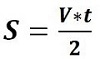 Kretanje rakete se posmatra kao pravolinijsko, jednako
ubrzano. Za njega kinematske jednačine brzine i pređenog
puta glase: v = a*t i S = v*t/2,
(v-brzina, S-put, a-ubrzanje i t-vrijeme).
Na rješavanje jednačina kretanja rakete primjenjuje se numerička
integracija. Numerička integracija razmatra veoma male intervale
promjena brzine i puta sa vremenom. Dovoljno male da aproksimacija
o pravolinijskom jednako ubrzanom kretanju daje zadovoljavajuće
rezultate. Jednačine kretanja primijenjene na male vremenske
intervale su date na slikama 3 i 4.
Kretanje rakete se posmatra kao pravolinijsko, jednako
ubrzano. Za njega kinematske jednačine brzine i pređenog
puta glase: v = a*t i S = v*t/2,
(v-brzina, S-put, a-ubrzanje i t-vrijeme).
Na rješavanje jednačina kretanja rakete primjenjuje se numerička
integracija. Numerička integracija razmatra veoma male intervale
promjena brzine i puta sa vremenom. Dovoljno male da aproksimacija
o pravolinijskom jednako ubrzanom kretanju daje zadovoljavajuće
rezultate. Jednačine kretanja primijenjene na male vremenske
intervale su date na slikama 3 i 4.
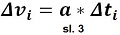
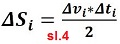 ΔSi je promjena puta u proizvoljnom
intervalu Δti , promjena brzine je
Δvi, a Δti
je proizvoljni interval vremena tokom numeričkog integraljenja putanje.
ΔSi je promjena puta u proizvoljnom
intervalu Δti , promjena brzine je
Δvi, a Δti
je proizvoljni interval vremena tokom numeričkog integraljenja putanje.
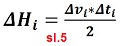 Ako se jednačine primijene na vertikalno, pravolinijsko, promjenljivo kretanje
onda je jednačina promjene puta (visine) ΔHi
kao na slici 5. Kinematske jednačine promjene visine i brzine rakete tokom
vertikalnog leta daju odnose brzine, ubrzanja, puta i vremena. Ako se zna
ubrzanje u nekom intervalu vremena može se izračunati prmjena brzine u
u tom intervalu,
Δvi = a*Δti .
Ako se zna promjena brzine može se izračunati pređena visina u tom intervalu
ΔHi = Δvi*
Δti/2.
Sabiranjem vremenskih intervala Δti
od početka kretanja do nekog proizvoljnog trenutka u toku leta
dobija se vrijeme leta ti do tog
trenutka. Sabiranjem promjena brzina
Δvi
u svim intervalima do nekog proizvoljnog intrvala i,
dobija se ukupna brzina u trenutku leta ti.
Sabiranjem promjena visine
ΔHi
u svim intervalima do nekog proizvoljnog intrvala i,
dobija se ukupna visina u trenutku leta ti.
Međutim, da bi se određivali pređeni put, brzina i vreijeme leta
potrebno je poznavati ubrzanje a kojem je podvrgnuta
raketa.
Prema Drugom Njutnovom zakonu ubrzanje, promjena brzine i
pravca su posledica dejstva spoljašnjih sila na tijelo, u ovom
slučaju raketu.
Ako se jednačine primijene na vertikalno, pravolinijsko, promjenljivo kretanje
onda je jednačina promjene puta (visine) ΔHi
kao na slici 5. Kinematske jednačine promjene visine i brzine rakete tokom
vertikalnog leta daju odnose brzine, ubrzanja, puta i vremena. Ako se zna
ubrzanje u nekom intervalu vremena može se izračunati prmjena brzine u
u tom intervalu,
Δvi = a*Δti .
Ako se zna promjena brzine može se izračunati pređena visina u tom intervalu
ΔHi = Δvi*
Δti/2.
Sabiranjem vremenskih intervala Δti
od početka kretanja do nekog proizvoljnog trenutka u toku leta
dobija se vrijeme leta ti do tog
trenutka. Sabiranjem promjena brzina
Δvi
u svim intervalima do nekog proizvoljnog intrvala i,
dobija se ukupna brzina u trenutku leta ti.
Sabiranjem promjena visine
ΔHi
u svim intervalima do nekog proizvoljnog intrvala i,
dobija se ukupna visina u trenutku leta ti.
Međutim, da bi se određivali pređeni put, brzina i vreijeme leta
potrebno je poznavati ubrzanje a kojem je podvrgnuta
raketa.
Prema Drugom Njutnovom zakonu ubrzanje, promjena brzine i
pravca su posledica dejstva spoljašnjih sila na tijelo, u ovom
slučaju raketu.
 U jednačini su F - rezultantna sila na tijelo u N,
m - masa tijela u kg i a - ubrzanje u m/s2.
Drugi Njutnov zakon može da se napiše i u drugom obliku (slika 6)
U jednačini su F - rezultantna sila na tijelo u N,
m - masa tijela u kg i a - ubrzanje u m/s2.
Drugi Njutnov zakon može da se napiše i u drugom obliku (slika 6)
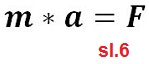 slijedi jednačina (slika 7), u kojoj se ubrzanje prikazuje kao
promjena brzina u intervalu vremena. Suština aproksimacije o
jednako ubrazanom kretanju ovdje je jasno prikazano. Ubrzanje
se mijenja tokom leta, ali u malom intervalu vremena uzima se
njegova srednja vrijednost i tako se može samo u njemu smatrati
konstantnim.
slijedi jednačina (slika 7), u kojoj se ubrzanje prikazuje kao
promjena brzina u intervalu vremena. Suština aproksimacije o
jednako ubrazanom kretanju ovdje je jasno prikazano. Ubrzanje
se mijenja tokom leta, ali u malom intervalu vremena uzima se
njegova srednja vrijednost i tako se može samo u njemu smatrati
konstantnim.
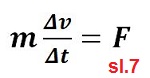 Ovo unosi grešku u proračun. Ukoliko je primijenjeni
interval vremena manji, greška je manja. Praksa je pokazala da se
dovoljna tačnost postiže ako je vremenski inerbal numeričke
integacije 0.001 - 0.01 sec za kretanje u lanseru
i 0.01 - 0.1 za slobodni dio putanje. Sa trenutnim
stanjem računarske tehnike vremenski interval numeričke integracije
može biti i manji, pa se postiže veća tačnost.
Ovo unosi grešku u proračun. Ukoliko je primijenjeni
interval vremena manji, greška je manja. Praksa je pokazala da se
dovoljna tačnost postiže ako je vremenski inerbal numeričke
integacije 0.001 - 0.01 sec za kretanje u lanseru
i 0.01 - 0.1 za slobodni dio putanje. Sa trenutnim
stanjem računarske tehnike vremenski interval numeričke integracije
može biti i manji, pa se postiže veća tačnost.
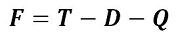 Sila F je rezultanta svih sila koje djeluju na raketu
tokom leta:
sile potiska T, sile otpora D i sile gravitacije Q.
Sila F je rezultanta svih sila koje djeluju na raketu
tokom leta:
sile potiska T, sile otpora D i sile gravitacije Q.
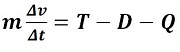 Njutnov zakon sada može da se prikaže u razvijenom obliku:
, a iz nje slijedi formula za promjenu brzine u proizvoljnom
intervalu vremena.
Njutnov zakon sada može da se prikaže u razvijenom obliku:
, a iz nje slijedi formula za promjenu brzine u proizvoljnom
intervalu vremena.
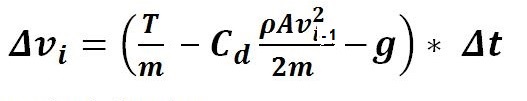

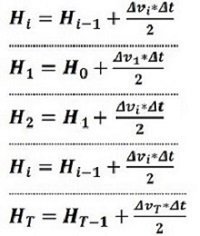
 ρ = 1.2 kg/m3, Cd = 1.75 za kupolu padobrana, A -
povšina padobrana je u m2, v - brzina propadanja u m/s,
a težina rakete W u gramima. Padobran je šestougani.
ρ = 1.2 kg/m3, Cd = 1.75 za kupolu padobrana, A -
povšina padobrana je u m2, v - brzina propadanja u m/s,
a težina rakete W u gramima. Padobran je šestougani.
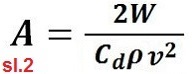 U momentu kada se otvori padobran uravnotežavaju se sila otpora
i težina rakete W, pa se iz jednakosti D = W.
dobija jednačina (sl.2) za površinu padobrana A koji se
spušta brzinom v. Iz vrijednosti površine
A izračunava se prečnik opisanog kruga šestouganog
padobrana.
U momentu kada se otvori padobran uravnotežavaju se sila otpora
i težina rakete W, pa se iz jednakosti D = W.
dobija jednačina (sl.2) za površinu padobrana A koji se
spušta brzinom v. Iz vrijednosti površine
A izračunava se prečnik opisanog kruga šestouganog
padobrana.
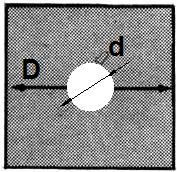
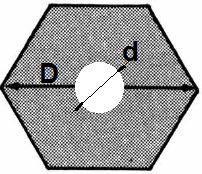
 Četvorougaona kupola nije pogodna za upotrebu. Osmougaona ima
previše padobranskih konopaca, pa je moguće njihov uplijetanje.
Okrugla kupola je nepodesna za pravilno rasporešivanje konopaca.
Šestougaona kupola je najčešće primjenjivano rješenje.
D je širina kupole (prečnik opisanog kruga).
Izračunava se uz pomoć priloženog kalkulatora, a u zavisnosti
od težine rakete i željene brzine spuštanja. Najpovoljnije
brzine spuštanja v su 4 - 6 m/s.
Manje vrijednosti iziskuju velike površine padobrana, pa se teško
pakuju u korisni prostor rakete. Veće brzine mogu biti opasne.
Površina padobrana se bira tako da se on lako pakuje, a da je
brzina spuštanja dovoljno mala za bezbjedno spuštanje. Primjetan
je manji otvor prečnika d u centru kupole . Taj
otvor obavezno treba napraviti, jer on vazduh struji kroz njega i
tako sprečava njihanje (ljuljanje) padobrana, odnosno daje stabilno
spuštanje. Prečnik d treba da iznosi 10%.
Četvorougaona kupola nije pogodna za upotrebu. Osmougaona ima
previše padobranskih konopaca, pa je moguće njihov uplijetanje.
Okrugla kupola je nepodesna za pravilno rasporešivanje konopaca.
Šestougaona kupola je najčešće primjenjivano rješenje.
D je širina kupole (prečnik opisanog kruga).
Izračunava se uz pomoć priloženog kalkulatora, a u zavisnosti
od težine rakete i željene brzine spuštanja. Najpovoljnije
brzine spuštanja v su 4 - 6 m/s.
Manje vrijednosti iziskuju velike površine padobrana, pa se teško
pakuju u korisni prostor rakete. Veće brzine mogu biti opasne.
Površina padobrana se bira tako da se on lako pakuje, a da je
brzina spuštanja dovoljno mala za bezbjedno spuštanje. Primjetan
je manji otvor prečnika d u centru kupole . Taj
otvor obavezno treba napraviti, jer on vazduh struji kroz njega i
tako sprečava njihanje (ljuljanje) padobrana, odnosno daje stabilno
spuštanje. Prečnik d treba da iznosi 10%.
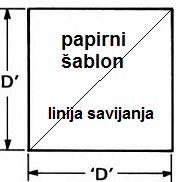
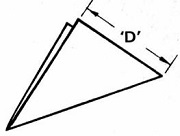
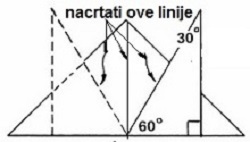
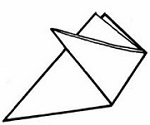

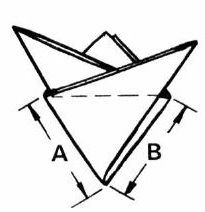
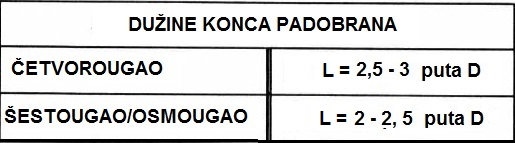
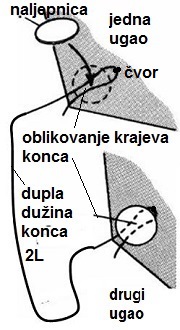 Konci padobrana se režu na duplu dužinu L, 2L.
Krajevi te duple dužine obliju se prema slici, postave na dva
susjedna ugla padobrana i pričvrste nalepnicama. Korisno je
napraviti čvor koji bi bio iznad naljepnice i bolje držao
konac od izvlačenja prilikom udara kod otvaranja padobrana.
Za šestougani padobran ovakvih konaca se napravi 3 komada.
Konci treba da su od prirodnog materijala koji ne gori, da
su dovoljno čvrsti i da su pogodni za manipulaciju. Ovo se
određuje iskustveno. Naljepnica mora biti čvrsto zalipljena
za ugao padobrana.
Konci padobrana se režu na duplu dužinu L, 2L.
Krajevi te duple dužine obliju se prema slici, postave na dva
susjedna ugla padobrana i pričvrste nalepnicama. Korisno je
napraviti čvor koji bi bio iznad naljepnice i bolje držao
konac od izvlačenja prilikom udara kod otvaranja padobrana.
Za šestougani padobran ovakvih konaca se napravi 3 komada.
Konci treba da su od prirodnog materijala koji ne gori, da
su dovoljno čvrsti i da su pogodni za manipulaciju. Ovo se
određuje iskustveno. Naljepnica mora biti čvrsto zalipljena
za ugao padobrana.
 Prije vezivanja konaca za uglove kupole obavezno
postaviti kružić.
Prije vezivanja konaca za uglove kupole obavezno
postaviti kružić.